Kataura plot was first introduced by Kataura et al. for the interpretation of resonant Raman spectra.

H. Kataura, Y. Kumazawa, Y. Maniwa, I Umezu, S. Suzuki, Y. Ohtsuka and Y. Achiba, Sythetic Metals 103 (1999), 2555-2558.

Later Saito et al. reported the detailed calculations of 1D electronic DOS with van Hove singularity in the following paper.

R. Saito, G. Dresselhaus, and M. S. Dresselhaus, Trigonal warping effect of carbon nanotubes, Physical Review B, vol. 61, no. 4, 2981 (2000).

All the detailed calculations are based on the above paper and you can find all the details and accurate discussions in the paper.

For my new students, I am preparing some simple visual material to help understanding of the paper. THIS IS UNDERCONSTRUCTION.

For the detailed discussions of Chirality and symmetry Click here.

For the calculated table of important parameters, Click here.

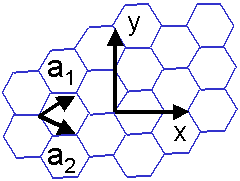
Hexagonal lattice in ordinal coordinates are summarized as below.

,

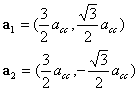
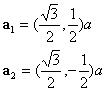
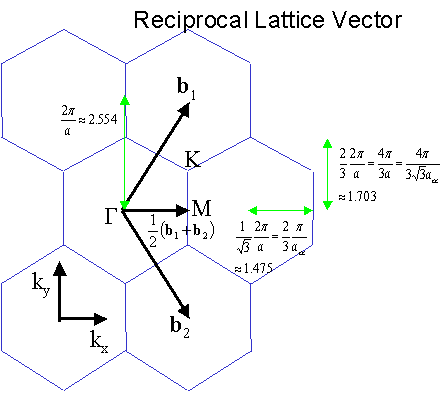
Now the reciprocal lattice vectors are defined as the figure below:

The conversions of base vectors are simply calculated as follows:

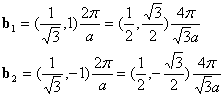
Brillouin Zone (central hexagonal area in the above figure) is expressed as follows:

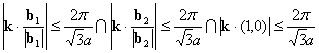
Chiral C_h and Lattice T vectors are transformed to K₁ and K₂ vectors as follows:

,

_,

Discrete unit vector along the circumferential direction:

Reciprocal lattice vector along the nanotube axis:

Let’s check the following:

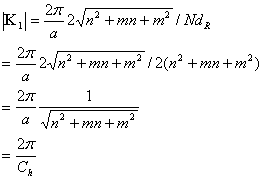
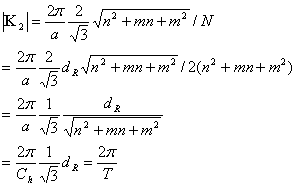
Note:

For a nanotube Brillouin Zone of graphite has no meaning and the k-space we should considered is as follows:

where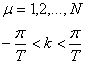

Hence,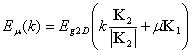

For tables of those value up to (40,40) nanotubes, click here.

The 2 D energy dispersion relations of graphite are shown as below.

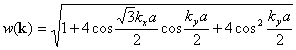
Overlap integral: s=0.129

Carbon-carbon interaction energy: g₀=2.9eV

e_2p = 0

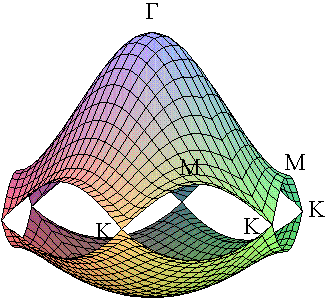
From: R. Saito, G. Dresselhaus, and M. S. Dresselhaus, Trigonal warping effect of carbon nanotubes, Physical Review B, vol. 61, no. 4, 2981 (2000).

[Color picture was from Professor R. Saito]

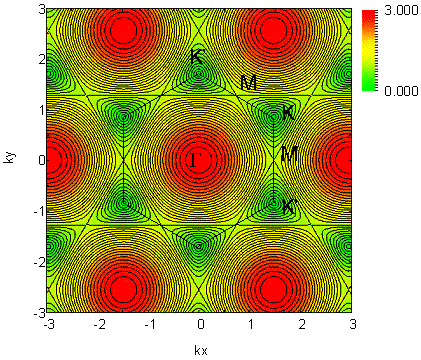
Or in the couture map of p and p* separately is shown as below:

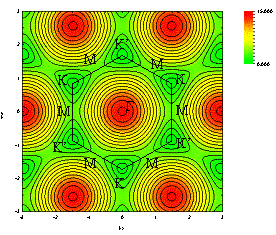
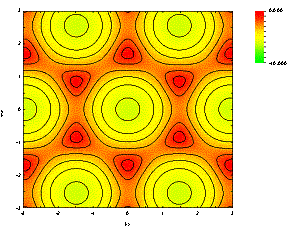
If you plot the value along K -> G -> M -> K, the dispersion is expressed as below:

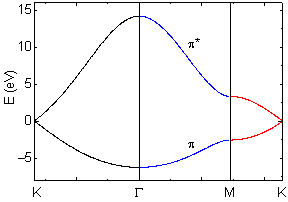
Asymmetry of conduction and valence bands is not important for the calculation of the energy difference of conduction and valence bands

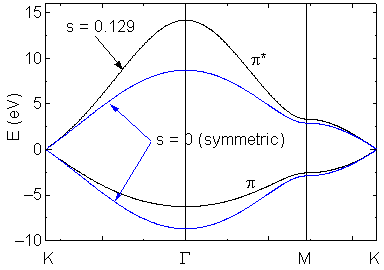
With s=0 and e_2p = 0

The dispersion relations is simplified as follows:

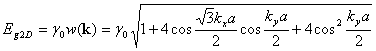
Compared with the asymmetric dispersion relations, the energy difference of p and p* bands of symmetric approximation are almost the same for low DE range such as 6 eV.

Hence, we can conclude the effect of overlap integral is not important.

The following calculations of DOS were performed for this symmetric dispersion relation.

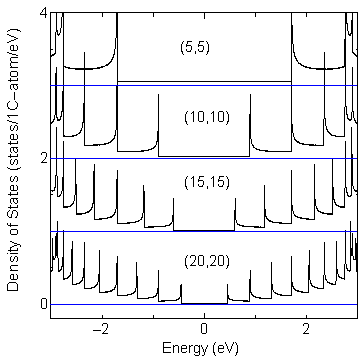
Examples of comparisons of DOS for armchair tubes

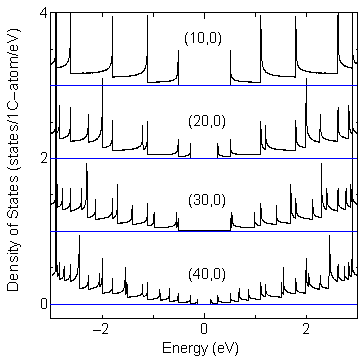
Examples of comparisons of DOS for zigzag tubes

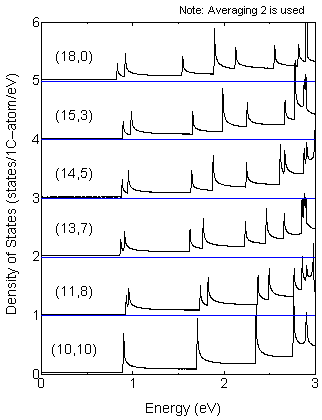
The trigonal warping effect (see the paper by R. Saito)

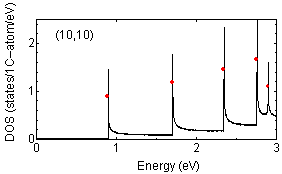
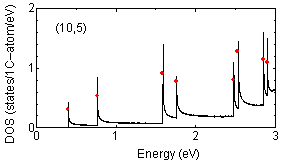
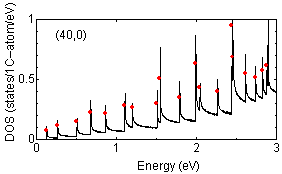
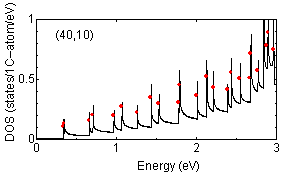
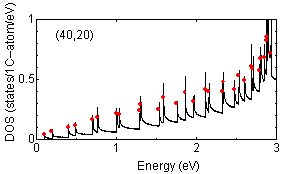
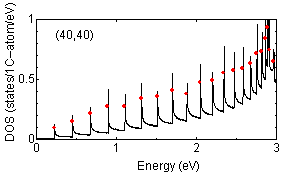
Examples of peak position findings are shown below:

The determination of van Hove singularity position is rather straightforward but the estimation of approximate height is more complicated. The red solid circles are assigned peak position with approximate height proportional to the strength of peaks.