丸山 茂夫(東大工)
Shigeo MARUYAMA, Eng.
Res. Inst., The University of Tokyo, 2-11-16 Yayoi, Bunkyo-ku,
Tokyo 113-8656
E-Mail:maruyama [at] photon.t.u-tokyo.ac.jp
URL:http://www.photon.t.u-tokyo.ac.jp/~maruyama/index-j.html
1.はじめに
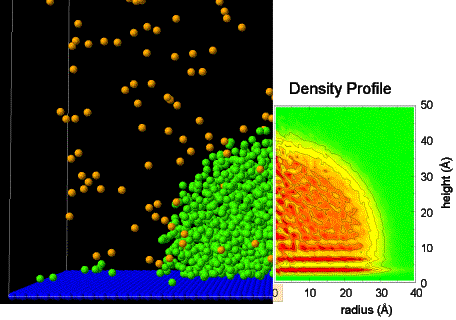
壁面上での液滴核生成の問題は,滴状凝縮理論の観点や最近の量子ドット生成などのナノテクノロジーとも関連して極めて興味深い.著者らは,図1に示すように,固体面上の液滴の平衡状態について分子動力学法を用いて検討してきており,分子スケールのポテンシャルパラメータと接触角などのマクロな測定量の関係を明らかにしてきた(1).一方,最近,L-J流体や水の均質核生成過程の分子動力学法による直接的なシミュレーションによって(2,3),古典核生成理論の限界が示されている.本報では固体壁面上での液滴の不均質核生成の分子動力学法シミュレーションを実行し,古典的な核生成理論との比較を示す.
[GIF Animation]
Fig. 1 A snapshot and density profile of liquid droplet on a
dolid surface.
Effect of temperature
and size.
2.計算方法
図2に示すように,下面に固体壁面を配置し,上面を鏡面,四方側面を周期境界条件とした系を考える.
[GIF Animation] Fig. 2 Calculation domain.
気体,液体分子はアルゴン分子を仮定して,Lennard-Jonesポテンシャル のパラメーター, 質量はアルゴンの値を用いる.
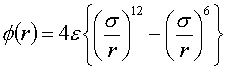 |
(1) |
壁面分子とアルゴンとのポテンシャルも Lennard-Jones ポテンシャルで表現し, 下壁面のエネルギーのパラメーターeINTを変化させ, 下壁面のぬれ易さを変化させた (表1参照) .
Table 1 Calculation conditions.
| Label | eINT [x10-21J] |
q [deg] |
Tave [K] |
Jsim [cm-2s-1] |
Jth [cm-2s-1] |
|---|---|---|---|---|---|
| E2 | 0.426 | 135.4 | 108 | 6.52x1020 | 4.86x1021 |
| E3 | 0.612 | 105.8 | 114 | 3.45x1021 | 4.47x1021 |
| E4 | 0.798 | 87.0 | 120 | 5.76x1021 | 5.54x1020 |
壁面はfcc <111>面のバネマス分子1層(4464個)とし,質量,最近接分子間距離,バネ定数はそれぞれ白金の値を用いた.更に,壁面分子の外側には温度一定のボルツマン分布に従うphantom分子を配置し,一定温度に保たれた熱浴を擬似的に実現した.その他の計算条件の詳細は,著者らが壁面での気泡生成のシミュレーションを行った場合とほぼ同様である(4).
3.結果と考察
初期条件として計算領域の中央に5760個のアルゴン分子をfcc構造で配置し,最初の100
psの間,設定温度(160 K)に応じた速度スケーリングによる温度制御を行った後,phantomによる温度制御のみで500
psまで計算して平衡状態のアルゴン気体で系を満たした.その後phantomの設定温度を100
Kに下げ,壁面から系を冷却していった.
表1のE2における圧力,温度,monomerの数,および最大クラスターサイズの時間変化を図3に示す.ここでクラスターとは各時間において分子間距離が1.2sAR以下であるような分子の集合と定義した.
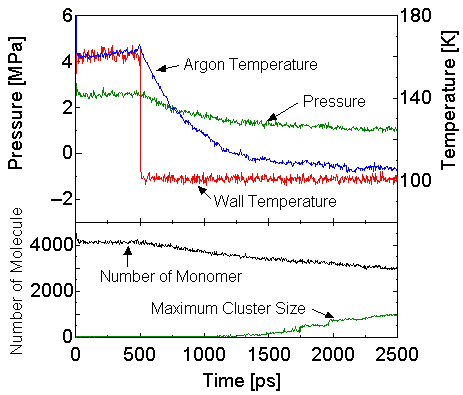
Fig. 3 Pressure, temperature, number of monomer,
maximum cluster size variations. (E2)
計算開始から500 ps後,phantomの温度制御により壁面が急激に冷却され,その後徐々にアルゴンの温度が下がっていく.その過程で徐々にクラスターが形成され,成長していく.
図4にクラスター生成の時間変化を示す.ここではより明瞭にするため5分子以上からなるクラスターのみを示した.
Fig. 4 Snapshots of clusters larger than 5 atoms.
生成するクラスターが壁面近傍に集中しているのがわかる.一方,よりぬれにくい壁面条件であるE1では液体内部においても比較的多くのクラスター生成が行われており,均質核生成に近い状況になっていた.
図5に閾値サイズ以上のクラスター数の時間変化を示す.破線はそれぞれが直線的に増加している部分にフィットするような直線である.
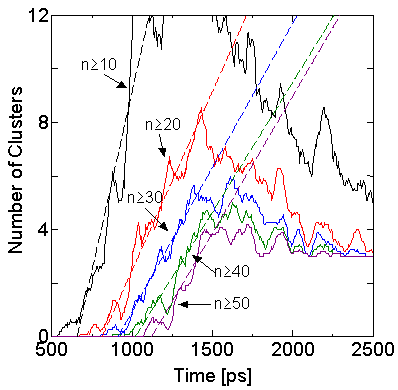
Fig. 5 Variations of number of clusters larger than a threshold.
(E2)
閾値20あるいは30以上ではこの直線の傾きがほぼ平行となっている.このことはそのサイズを超えたクラスターが安定的に成長を続けていることを示しており,この直線の勾配から核生成速度を見積もることができる.30以上,40以上,50以上の直線の傾きの平均から見積もられる核生成速度はJsim = 3.45x1021 cm-2s-1となる.
一方,古典核生成理論では平滑な固体壁面での不均質核生成の核生成速度Jthは以下のように表すことができる.
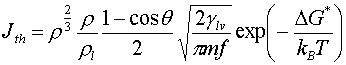 |
(2) |
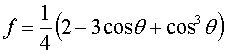 |
クラスター数が直線的に変化している1000 psから1500 psの平均温度Tave,およびmonomerの密度rを用いて計算を行うと,Jth = 4.47x1021 cm-2s-1となる.均質核生成の場合に7桁もの大きな差があったのに反して,本シミュレーションでは理論と非常によく一致している.また臨界クラスターサイズは
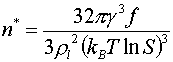 |
(3) |
で与えられ,n* = 16.5と計算される.シミュレーションからは図 5における直線の傾きの変化から20程度が臨界クラスターのサイズであると見積もられ,ほぼ一致する.
臨界核以下のクラスター分布は
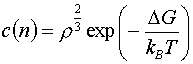 |
(4) |
で与えられる.この式を用いてシミュレーションで得られるクラスター数が直線的に変化している期間の平均クラスター分布c(n)からクラスター生成に必要な自由エネルギーDGを求めたのが図6の丸印である.実線は理論で以下の式で与えられるDGを示す.
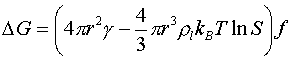 |
(5) |
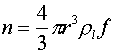 |
また,三角は壁面に接触していないクラスター分布から求められるDG,点線は均質核生成の場合の理論式から導かれるDGを示す.
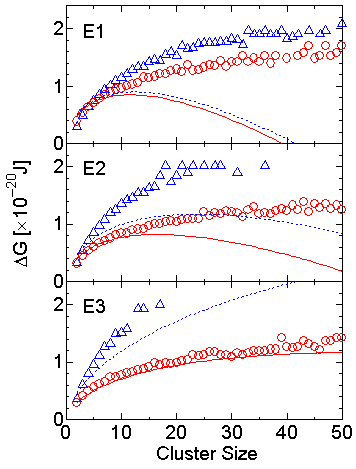
Fig. 6 Cluster formation free energy.
ここで式(4)によるDGの見積もりは臨界核(DGがピークの位置)以下のサイズでのみ有効である. 壁面がぬれやすくなるほど,壁面に接するクラスターと接しないクラスターのDGの差が大きくなる.臨界核以下の部分で比較すると不均質核生成の理論と壁面に接するクラスター分布から得られるDGはほぼ一致していることがわかる.一方,均質核生成理論から得られるものと壁面に接触していないクラスター分布とでは,若干シミュレーションのクラスター分布から得られるDGが大きくなっているものの,全体としての一致は均質核生成のMDシミュレーションの結果からは考えられないほどよい.
5 おわりに
固体壁面を急冷することによる液滴の不均質核生成の分子動力学法シミュレーションによって,古典核生成理論とそれほど違わない核生成速度が計算された.均質核生成の分子動力学法では,古典核生成理論とほど遠い結果となっていることから,本報の系での核生成速度の一致は予想に反するものであり,その理由の解明は今後の課題となる.ただし,いずれの分子動力学法シミュレーションも現実的なマクロな熱問題の時間スケールや過飽和度と相当に異なる条件であり,マクロな問題との直接的な比較は容易ではない.
文献
(1) Maruyama, S., ほか4名, Microscale Thermophysical
Engineering, 2-1 (1998), 49-62.
(2) Yasuoka, K. & Matsumoto, M., J. Chem. Phys., 109-19 (1998),
8451-8462.
(3) Yasuoka, K. & Matsumoto, M., J. Chem. Phys., 109-19 (1998),
8463-8470.
(4) 丸山茂夫・木村達人, 機論, 65-638 B (1999), 225-231.