ICHMT Symposium Molecular & Microscale Heat Transfer,

Yokohama, Dec. 1-5, 1996.

ABSTRACT. The formation mechanism of fullerene, a new type of carbon molecule with hollow caged structure, was studied using the molecular dynamics method with the simplified classical potential function. The clustering process starting from isolated carbon atoms was simulated under controlled temperature condition. Here, translational, rotational and vibrational temperatures of each cluster were controlled to be equilibrium. The structure of clusters obtained after enough calculation depended on the controlled temperature T_c, yielding to graphitic sheet for T_c < 2600 K, fullerene-like caged structure for 2600 K < T_c < 3500 K, and chaotic 3-dimensional structure for T_c > 3500 K. Through the detailed trace of precursors, it was revealed that the key feature of the formation of the caged structure was the chaotic 3-dimensional cluster of 40 to 60 atoms which had large vibrational energy. On the other hand, when precursors were kept under lower vibrational energy, the successive growth of 2-dimensional graphitic structure was observed. Since the time scale of the simulation was compressed, the annealing process of each cluster was virtually omitted. In order to examine this effect, an imperfect C₆₀ obtained from the similar simulation was annealed at 2500 K for 50 ns without collisions. The perfect Buckminsterfullerene C₆₀ was finally obtained after successive Stone-Wales transformations.

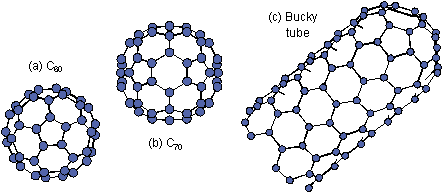
Existence of soccer-ball structured C₆₀ shown in Fig. 1.1 (a) was demonstrated by Kroto et al. (1985) through their time-of-flight mass spectra of carbon clusters generated by the laser-vaporization supersonic-nozzle technique. They observed a prominent C₆₀⁺ signal and the complete lack of odd-numbered clusters. They named the cluster C₆₀ of truncated icosahedron Buckminsterfullerene since the beautiful network structure resembled the famous geodesic dome designed by Buckminster Fuller. Since mass spectra of positive carbon clusters exhibited only even numbered clusters in the range of C₃₀ to at least C₆₀₀ [Rohlfing et al. (1984) and Maruyama et al. (1991)], we could speculate that all of those clusters had polyhedral structure. Carbon clusters with such hollow close-caged structure are called fullerene [Fig. 1.1]. In 1990, discoveries of simple techniques for macroscopic generation and isolation of fullerene by Krtschmer et al. (1990), Haufler et al. (1991) and Taylor et al. (1990) had made this new material ready for applications among many fields. The observation of the superconductivity by Hebard et al. (1991) at T_c = 19 K of potassium-doped C₆₀ crystal further accelerated the research field. Within a few years, macroscale amount of metal containing fullerene [Chai et al. (1991), Shinohara et al. (1992) and Kikuchi et al. (1993)], higher fullerenes [Kikuchi et al. (1992) and Achiba & Wakabayashi (1993)] and bucky tube in Fig. 1.1(c) [Iijima (1991) and Ebbesen & Ajayan (1992)] were available.

A common technique of the macroscopic generation of fullerene is the arc-discharge method which is simply an arc-discharge of graphite electrodes under certain pressure of helium buffer gas condition proposed by Haufler et al. (1991). The amount of extracted fullerene compared to the collected soot can yield up to about 15% under the optimum condition such as Maruyama et al. (1994b). Usually the generated fullerene consists of 80% of C₆₀, 15% of C₇₀ and a small amount of higher fullerene like C₇₆, C₇₈, C₈₂, C₈₄, .., quite interesting magic numbers. It is also surprising that once vaporized carbon atoms automatically form such highly symmetric structures like C₆₀ in the clustering process. Besides these theoretical interests, it is required to clarify the generation mechanism in order to find a more efficient generation method of the higher fullerene or the metal doped fullerene.

Since the macroscale generation technique was found accidentally, the formation mechanism of fullerene is not clear. Several models have been proposed based on experimental insights. Haufler et al. (1991) described that a growth of a hexagonal network by successive additions of dimers and trimers eventually left pentagons as the defect. They claimed that the pentagons was essential to give the curvature and to decrease the number of dangling bonds. On the other hand, two neighboring pentagons should result in too much strain to the network system, so the Isolated Pentagon Rule (IPR) was assumed. It is interesting to learn that the smallest fullerene satisfying IPR is C₆₀ and next to the smallest is C₇₀. Quite different precursors of fullerene structure were proposed, such as a piece of graphitic sheet [Robertson et al. (1992)] or once grown bucky tube [Dravid et al. (1993)]. On the other hand, Heath (1992) proposed a model of clustering sequence from linear chain up to C₁₀, rings in C₁₀-C₂₀ range, fullerene at C₃₀. He explained that successive C₂ additions followed until the satisfaction of IPR. Wakabayashi & Achiba (1992) proposed a special model that fullerene was made of stacking of carbon rings. They could explain magic numbers of higher fullerenes [Kikuchi et al. (1992) and Achiba & Wakabayashi (1993)] and isomers of C₇₆, C₈₆ and C₈₄ [Wakabayashi et al. (1993)]. Recently, the drift tube ion chromatography experiments of laser vaporized carbon clusters showed the existence of poly-cyclic rings and the possibility of the annealing of such structure to fullerene [Helden et al. (1993), Hunter et al. (1993), Clemmer et al. (1994) and Hunter et al. (1994)].

Although each model can explain some experimental results, it is difficult to decide which model is more plausible. We have applied the molecular dynamics method to simulate the clustering process of carbon atoms in order to speculate the formation process of fullerene from a different point of view. Our previous result [Maruyama & Yamaguchi (1995b)] showed the possibility of simulating the fullerene formation process from the randomly distributed carbon atoms. However, since the temperature control was rather arbitrary, the comparison with the physical phenomena was not easy and no perfect fullerene was obtained. In this study, we have performed the similar simulations with more sophisticated temperature control and considered the importance of cooling rate and annealing.

The classical molecular dynamics method was employed for the simulation. There were two major difficulties to overcome in this simulation. One was the assumption of the many-body potential function for carbon atoms. Since the whole process involved the chemical reaction and the bonding of carbon atoms could be varied from sp, sp² and sp³, we could not expect a reliable classical formulation of many-body potential. We employed the potential function developed by Brenner (1990) and ignored the sophisticated conjugate term, because the tough and qualitative function was more plausible than the quantitative but delicate potential function.

Another difficulty was the intrinsic long time scale of the physical process. The laser-vaporization supersonic nozzle experiments suggested that the time scale of the formation of fullerene was about 100 microseconds [Maruyama et al. (1990)]. Probably, the time scale was longer for the arc-discharge method. Then, the direct molecular dynamics simulation of full time scale is far from possible even for the fastest supercomputers. Our choice was the compression of the time scale, simply by assuming the high number density of initial carbon atoms. This assumption forced us the extremely painful modifications of the boundary conditions and very careful appreciation of the simulated results. We assumed that the process could be divided into 3 major procedures: 1) Collisions of atoms or clusters with each other which would result in the growth of cluster or sometimes fragmentation; 2) Cooling of clusters by the continuous collisions with buffer gas molecules and radiation; 3) Annealing of each cluster in between collisions. The high density meant that the rate of procedure 1) was much increased. Then, we assumed the rate of procedure 2) should be increased accordingly. Because the long time scale of the real system should imply the relatively equilibrium distribution of kinetic energy to translational, rotational and vibrational energy, we used the temperature control method which included the strong tendency toward the equilibrium. Finally, the effect of procedure 3) was very much underestimated. We tried to estimate the effect of the annealing in the separate simulation.

2.1 Many-Body Potential Function

We have employed the potential function proposed by Brenner (1990), originally used for his simulation of CH₄ CVD (chemical vapor deposition) of the diamond film. This potential was based on the Tersoff's (1986) bond-order expression and was modified to describe the variety of small hydrocarbons, graphite, and diamond lattice. The total energy of the system E_b was described as the sum of the bonding energy of each bond between atom i and j.

(2.1)

where V_R(r) and V_A(r) were repulsive and attractive force terms, respectively. Morse-type exponential functions with a cut-off function f(r) were used for these functions.

(2.2)

(2.3)

(2.4)

The state of the bonding was expressed through the term B* as the function of angle between bond i-j and each neighboring bond i-k.

(2.5)

where

(2.6)

Since small carbon clusters were not taken into account for Brenner's simulation, the clustering process from small clusters to poly-cyclic bond-network structures could not be simulated [Maruyama & Yamaguchi (1995a)]. In order to compensate it, we have ignored the conjugate-compensation term F which was included in the Brenner's original expression. Constants were as follows.

D_e = 6.325 eV S = 1.29 = 1.5 Å^-1 R_e = 1.315 Å

R₁ =1.7 Å R₂ = 2.0 Å.

= 0.80469 a₀ = 0.011304 c₀ = 19 d₀ = 2.5

Simple Verlet's method was adopted to integrate the classical equation of motion with its time step of 0.5 fs.

2.2 Temperature Control Technique

A cluster was defined as a group of carbon atoms inter-connected one another with C-C bonds. Here, the C-C bond was defined between 2 carbon atoms whose distance was smaller than the cut-off distance R₂. The kinetic energy of a cluster C_n with n carbon atoms was divided into translational K_T, rotational K_R and vibrational energy K_V. Each energy was expressed as

, , (2.7)

where m was the mass of the carbon atom, and were relative position and relative velocity of each atom i from the mass center position and velocity , respectively. The corresponding temperatures of each cluster and the total system T^total which was expressed as the weighted average of N clusters were

, , (2.8)

, , (2.9)

, , (2.10)

where n was the number of freedom of each motion of a cluster, and k_B was Boltzmann constant.

As described previously, we tried to enforce the equilibrium of translational, rotational and vibrational temperature of the system in order to incorporate the compression of the time scale by the increase of the number density of carbon atoms. In this calculation, each temperature of the system was independently controlled every 0.1 fs through simple velocity scaling so that the difference between present temperature of the system and control temperature was reduced to 60 %.

In order to determine the characteristics of the potential function when applied to fullerene, high temperature stability of the structure of Buckminsterfullerene C₆₀ [Fig. 1.1 (a)] was examined. Sixty carbon atoms were located at the equilibrium position of the truncated icosahedron C₆₀ as the initial condition. Then, the vibrational motion was simulated at various control temperature T_c for 1 ns.

Fig. 3.1 summarizes the observed structure after 1ns at each temperature. For clarity, bond-network structures were expressed as two-dimensional maps for the hollow caged structures in Fig. 3.1 (a-d). When the temperature was below 2500 K, no change of network structure was observed within 1 ns [Fig. 3.1 (a)]. Shaded pentagons should help to check the characteristics of truncated icosahidran, twelve isolated pentagons and 20 hexagons in accordance to IPR. Slight deformation of the network structure was noticeable for T_c = 2600 K in Fig. 3.1 (b). The isomerization by concerted transformations was observed as discussed later. For 2600 K < T_c < 3000 K, transformations occurred more frequently but principally keeping the 5-6 network structure. At T_c = 3000 K, dangling bonds for atoms marked by empty symbols were seen as Fig. 3.1 (c). With these dangling bonds, much more violent and continuous reactions were observed. At T_c = 3200 K, several dangling bonds were moving around the network [Fig. 3.1 (d)]. When the temperature was 3500 K, the caged structure was partially broken with a large hole [Fig. 3.1 (e)], and then, transformation to a chaotic 3-dimensional cluster was observed in Fig. 3.1 (f) at T_c = 4000 K. At T_c = 5000 K, a part of cluster was dissociated from the main body [Fig. 3.1 (g)], and when the temperature was as high as 6000 K, the main body could not keep the size and divided into several small clusters [Fig. 3.1 (h)].

Fig. 3.2 shows the detailed process of the pentagon-migration transformation observed at 2600 K [Fig. 3.1 (b)]. Until 19.5 ps the network structure kept perfect C₆₀. From 19.5 ps through 20 ps, bonds marked A-B and C-D were broken and a new bond A-C was created, leaving dangling bonds on atom B and D [Fig. 3.2 (b)]. Then, B chose atom D as a new bond partner at t = 20.5 ps [Fig. 3.2 (c)]. During this process, the line connecting 4 atoms marked by empty symbol in Fig. 3.2 were merely twisted without the breakage. The whole process could be regulated as a simple migration of pentagons without the change of the total number of pentagons and hexagons. This process known as Stone-Wales transformation or pyracylene rearrangement has been argued as a possible path of isomerization of carbon clusters [Stone & Wales (1986)].

We have shown the similar results previously [Maruyama & Yamaguchi (1995b)], where the total energy of the system was kept constant and calculated only for 100 ps. Previous results showed that no isomerization was observed up to 3000 K. Since the difference of temperature control should have minor effect in this calculation, the difference of the observation time should be the reason of the discrepancy. If we assume the Arrhenius type of reaction rate for the isomerization process, this discrepancy can be explained that with longer time we have more chance to see the isomerization process. Since the activation energy was about 3 eV by this simulation, the rough extrapolation of the time scale to seconds (10⁹ ns) will give the order of 1000 K for the onset of the isomerization which is in good agreement with experimental knowledge. Furthermore, it is suggested that the compression of time must be accompanied with the proper increase of temperature in order to reproduce the reasonable reaction.

The most interesting point about the formation mechanism of fullerene is how such a hollow caged structure could be self-assembled. As seen in the previous section, fullerene structure is extraordinary stable, even though the 2500 K must be over-estimated, and we supposed the high temperature stability would be the key of the preference of fullerene compared to diamond or graphite structure. Although we have already demonstrated that the clustering process of caged structures and flat structures by using this potential function [Maruyama & Yamaguchi (1995b)], it was difficult to evaluate the effect of temperature and density because of the inequilibrium of temperature caused by the previous temperature control method. Then, we applied a new temperature control method and calculated the clustering process under the artificial equilibrium condition.

1. Structure of Generated Clusters

As an initial condition, 200 carbon atoms with random velocity were located at random positions in a 8 nm cubic box with full periodic boundary conditions. Then, translational, rotational and vibrational temperature of the system was independently controlled toward a constant temperature T_c by the technique in the previous section. Several snapshots of the simulation for T_c = 3000 K are shown in Fig. 4.1. At 20 ps, most clusters were smaller than C₃, while several chain clusters as large as C₁₀ were observed. At about t = 60 ps, some of clusters grew to ring or chain structure with about 12 atoms, and the largest cluster C₂₅ formed a poly-cyclic network structure. A chaotic 3-dimensional structures C₃₇, C₄₅, C₄₉ and flat structure C₆₂ appeared at t = 120 ps, and finally at t = 300 ps, a large tube-like cluster as large as C₁₆₀ with hollow caged structure mainly consisted of pentagons and hexagons was obtained. Through the process, the equilibrium of the temperature was realized except for the initial 50 ps when the released potential energy was extremely large compared to the cluster size.

Fig. 4.2 shows the representative clusters observed for various temperature conditions after 300 ps calculation. For T_c = 1000 K, the cluster had almost complete 2-dimensional structure though some large rings remained [Fig. 4.2 (a)]. For T_c = 2000 K as shown in Fig. 4.2 (b), small poly-cyclic rings had coalesced to a graphitic network structure consisted of 2 flat components and an irregular part at the middle. When the control temperature was 2600 K, the cluster constructed a imperfect cage structure with a large hole [Fig. 4.2 (c)]. And for T_c = 3000 K, a hollow caged structure without large holes was observed [Fig. 4.2 (d)]. For higher temperature as T_c = 3500 K [Fig. 4.2 (e)], the clusters could not keep any regular structure and transformed to chaotic 3-dimensional structure including several carbon atoms with four bonds. For T_c = 6000 K, the clusters could not keep large size due to the dissociation process and formed simpler structures [Fig. 4.2 (f)]. Under very high temperature condition as T_c = 8000 K [Fig. 4.2 (g)], the clusters could not grew large and formed some small simple structures such as chains or single rings up to about C₂₀.

4.2 Precursors in the Reaction Process

The clustering process was examined in detail with the special attention to the structure and vibrational temperature of precursors. The clustering process yielding to a caged structure for T_c = 3000 K are shown in Fig. 4.3 (a). Precursor clusters smaller than C₂₀ had simple structure basically constructed of chains and a few rings. The coalescence of these small pieces resulted in the random chaotic 3-dimensional structure around C₄₀. Then, a rather complex transformation to a spherical structure of around C₅₀ followed [marked (2) in Fig. 4.3 (a)]. At the same time, another large cluster C₆₄ had the flat graphitic structure. The collision of these two clusters [mark (3) in Fig. 4.3 (a)] and annealing [mark (4) in Fig. 4.3 (a)] resulted in the caged structure of C₁₆₀.

The bottom diagram shows the vibrational temperature T_v and the bond-switching rate R_s for the marked clusters. The parenthesized mark on top and bottom panel corresponds in time. Here, the bond switching rate R_s was defined as the number of bond creation and breakage in a cluster in 1 ps divided by the number of atoms of the cluster. The small clusters with larger vibrational energy frequently switched the bond-network structure, and grew to larger cluster before the stabilization of the structure [mark (1) in Fig. 4.3 (a)]. The process marked as (2) in Fig. 4.3 (a) shows the rapid annealing and decrease of the bond-switching rate toward C₅₀. The bond-switching rate is rather small after the middle of the process marked (2) compared to the smaller clusters, implying that the gradual annealing of semi-caged cluster.

On the other hand, the clustering process yielding to a graphitic structure was very simple as shown in Fig. 4.3 (b). The precursors always formed flat structure and extended the size in 2-dimensional direction at T_c = 1000 K. During the whole process, the clusters had low vibrational temperature and changed the network structure only in the case of the collision and only around the contact point in order to organize the flat structure.

4.3 Transition of Cluster Size Distribution

Although the selectivity of the caged structure in the certain temperature range is explained in the previous section, it is still unknown why C₆₀ is so preferable than other sized fullerene. About 80 % of generated fullerene are C₆₀ for typical arc-discharge method. On the other hand, the percentage of C₆₀ in fullerene generated in laser-vaporization cluster source is usually less than 0.1 %. The key mechanism of C₆₀ selection must explain this difference. We considered that the annealing of clusters should give a hint to this question. The simulation shown in Fig. 4.3 (a) cannot be regarded as successful, because the final collisions of C₅₀ size range clusters have made too large cluster, C₁₆₀.

In order to estimate the time scale for annealing, we have considered the collision rate and collisional cross section of each cluster. The transition of cluster size distribution for T_c = 3000 K is shown in Fig. 4.4. Here, the time traces of typical large clusters are described. Long vertical lines apparent in Fig. 4.4 mean the collision free period. These long lines appeared when the cluster size grew to about C₄₀ - C₆₀ especially with 3-dimensional structure. This is related to the decrease of the collisional cross-section by the transformation to the compact 3-dimensional structure. As a consequence these 3-demensional clusters can get enough time for annealing toward the perfect fullerene structure which would be stable enough to reject further reactions even with later collisions.

1. EFFECT OF ANNEALING

Considering the time scale compression in this simulation, the time scale of the annealing process appeared in Fig. 4.4 can correspond to tens of micro-seconds in practice. In order to evaluate the effect of annealing process, we have picked up an imperfect C₆₀ caged cluster obtained in our previous similar simulation [Maruyama & Yamaguchi (1994a)], and simulated the annealing process without collision. The temperature was controlled at T_c = 3000 K for first 8 ns to promote rapid annealing, then set at T_c = 2500 K for about 50 ns afterwards. The transition of bond-network structure is summarized in Fig. 5.1. Here, shaded and empty faces are pentagons, and hexagons, respectively, heptagonal faces are marked as 7, empty symbols are atoms with dangling bonds. The initial cluster included 4 dangling bonds and 8 heptagons [Fig. 5.1 (a)]. The number of these defects gradually decreased until 15 ns [Fig. 5.1 (c)], where all dangling bonds were terminated and no heptagons remained. A clear correspondence can be seen in the potential energy per atom in bottom picture. Then, the bond-network could gradually changed through Stone-Wales transformation without the inclusion of heptagons or dangling bonds. However, there were rather violent reconstruction of whole network structures at around 18 ns [Fig. 5.1 (c)] and 34 ns. There were only successive Stone-Wales transformations after about 37 ns [Fig. 5.1 (e)] toward the final perfect Buckminsterfullerene C₆₀ in Fig. 5.1 (f). We believe that the violent reconstruction is due to a little too high temperature of the simulation and is not necessary for the real physical annealing process.

A molecular dynamics simulation of the clustering process starting from randomly distributed carbon atoms yielded to the imperfect fullerenes under certain high temperature control. On the other hand, flat graphitic sheets were generated under low temperature condition. The caged structure was shaped through the annealing of chaotic 3-dimensional precursors around C₅₀ with small surface area, in contrast with the consecutive growth mechanism of graphitic sheet. The 3-dimensional clusters around C₅₀ could form a more sophisticated structure through their long lifetime due to the small collisional cross section. Although the simplified potential and the time-scale compression technique made it difficult to compare the simulation with experimental results, we could demonstrate the formation of fullerene completely through the self-assembly of carbon atoms. Furthermore, the possible annealing process to the perfect Buckminsterfullerene C₆₀ was demonstrated. These results would indicate the possible path of clustering to fullerene.

B^*: Normalized bond order function

D: Potential well depth

E_b: Bonding energy

f: Cut-off function

K: Kinetic energy

k_B: Boltzmann constant

m: Mass of carbon

n: Number of molecules of a cluster

R_s: Bond switching rate

R: Lattice constant

r_ij: Distance between atom i and atom j

r: Position vector

S: Potential parameter

T: Temperature

T_c: Control temperature

t: Time

V: Potential function

v: Velocity vector

Greek Symbols

: Potential parameter

: Potential parameter

: Number of freedom of cluster motion

: Angle

Subscripts

A: Attractive

e: Equilibrium

V: Vibrational

R: Rotational or repulsive

T: Translational

We thank Professor Emeritus Susumu Kotake at the University of Tokyo for his kind discussions during this study. This work was supported by a Grant-in-Aid for Scientific Research from the Ministry of Education, Science and Culture, Japan.

Achiba, Y. & Wakabayashi, T., 1993, "Stability, Structures and Hypothetical Growth Mechanism of Carbon 5/6 Network," Z. Phys. D, 26, 69-73.

Brenner, D. W., 1990, "Empirical Potential for Hydrocarbons for Use in Simulating the Chemical Vapor Deposition of Diamond Films," Phys. Rev. B, 42-15, 9458-9471.

Chai, Y. et al., 1991, "Fullerenes with Metals Inside," J. Phys. Chem., 95, 7564-7568.

Clemmer, D. E. et al., 1994, "Gas-Phase Self-Assembly of Endohedral Metallofullerenes," Nature, 367, 718-720.

Dravid, V. P. et al., 1993, "Buckytubes and Derivatives: Their Growth and Implications for Buckyball Formation," Science, 259, 1601-1604.

Ebbesen, T. W. & Ajayan, P. M., 1992, "Large-Scale Synthesis of Carbon Nanotubes," Nature, 358, 220-222.

Haufler, R. E. et al., 1991, "Carbon Arc Generation of C₆₀," Mat. Res. Soc. Symp. Proc., 206, 627-638.

Heath, J. R., 1992, "Synthesis of C₆₀ from Small Carbon Clusters, A Model Based on Experiment and Theory," Fullerenes, Ed. G. S. Hammand & V. J. Kuck, American Chemical Society (Washington, D. C.), 1-23.

Hebard, A. F. et al., 1991, "Superconductivity at 18K in Potassium-Doped C₆₀," Nature, 350, 600-601.

Iijima, S., 1991, "Helical Microtubules of Graphitic Carbon," Nature, 354, 56-58.

Helden, G. et al., 1993, "Experimental Evidence for the Formation of Fullerenes by Collisional Heating of Carbon Rings in the Gas Phase," Nature, 363, 60-63.

Hunter, J. et al., 1993, "Annealing C₆₀⁺: Synthesis of Fullerenes and Large Carbon Rings," Science, 260, 784-786.

Hunter, J. M. et al., 1994, "Annealing Carbon Cluster Ions: A Mechanism for Fullerene Synthesis," J. Phys. Chem., 98-7, 1810-1818.

Kikuchi, K. et al., 1992 "Isolation and Identification of Fullerene Family: C₇₆, C₇₈, C₈₂, C₈₄, C₉₀ and C₉₆," Chem. Phys. Lett., 188-3,4, 177-180.

Kikuchi, K. et al., 1993 "Isolation and Characterization of the Metallofullerene LaC₈₂," Chem. Phys. Lett., 216-1,2, 23-26.

Krtschmer, W. et al, 1990, "Solid C₆₀: a new form of carbon," Nature, 347, 354-358.

Kroto, H. W. et al., 1985, "C₆₀: Buckminsterfullerene," Nature, 318-6042, 162-163.

Maruyama, S. et al., 1990, "Direct Injection Supersonic Cluster Beam Source for FT-ICR Studies of Clusters," Rev. Sci. Instrum., 61-12, 3686-3693.

Maruyama, S. et al., 1991, "Thermionic Emission from Giant Fullerenes," Z. Phys. D, 19, 409-412.

Maruyama, S. et al., 1994a, "A Molecular Dynamics Simulation for the Formation Mechanism of Fullerene," Proc. 31st National Heat Transfer Conf., 940-942.

Maruyama, S. et al., 1994b, "The Effect of Helium Convection on the Generation Process of Fullerene," Proc. 31st National Heat Transfer Conf., 943-945.

Maruyama, S. & Yamaguchi, Y., 1995a, "A Molecular Dynamics Simulation for the Formation Process of Fullerene (Part 2)," Proc. 32nd National Heat Transfer Conf., 839-840.

Maruyama, S. & Yamaguchi, Y., 1995b, "A Molecular Dynamics Simulation for the Formation Mechanism of Fullerene," Therm. Sci. & Engng., 3-3,105-109.

O'Brien S. C. et al., 1988, "Photophysics of Buckminsterfullerene and Other Carbon Cluster Ions," J. Chem. Phys., 88-1, 220-230.

Robertson, D. H. et al., 1992, "On the Way to Fullerenes: Molecular Dynamics Study of the Curling and Closure of Graphitic Ribbons," J. Phys. Chem., 96, 6133-6135.

Rohlfing, E. A. et al., 1984, "Production and Characterization of Supersonic Carbon Cluster Beams," J. Chem. Phys., 81-7, 3322-3330.

Shinohara, H. et al., 1992 "Mass Spectroscopic and ESR Characterization of Soluble Yttrium-Containing Metallofullerenes YC₈₂ and Y₂C₈₂," J. Phys. Chem., 96, 3571-3573.

Smalley, R. E., 1993, "From Dopyballs to Nanowires," Materials Science and Engineering, B19, 1-7.

Stone, A. J. & Wales, D. J., 1986, "Theoretical Studies of Icosahedron C₆₀ And Some Related Species" Chem. Phys. Lett., 128, 501-503.

Taylor, R. et al., 1990, "Isolation, Separation, and Characterization of the Fullerenes C₆₀ and C₇₀: The Third Form of Carbon," J. Chem. Soc. Chem. Communications, 1423, 1423-1425.

Tersoff, J., 1986, "New Empirical Model for the Structural Properties of Silicon," Phys. Rev. Lett., 56-6, 632-635.

Wakabayashi, T. & Achiba, Y., 1992, "A Model for the C₆₀ and C₇₀ Growth Mechanism," Chem. Phys. Lett., 190-5, 465-468.

Wakabayashi, T. et al., 1993, "A Selective Isomer Growth of Fullerenes," Chem. Phys. Lett., 201-5,6, 470-474.