日本機械学会論文集B編投稿中
*1 正員,東京大学大学院工学系研究科機械工学専攻(〒113 東京都文京区本郷7-3-1)
*2 正員,同上
The formation mechanism of Fullerene,
a new type of carbon molecule with hollow caged structure, was
studied using the molecular dynamics method with the empirical
potential function. The clustering process starting from isolated
carbon atoms was simulated under the controlled temperature condition,
where translational, rotational and vibrational temperature of
each cluster was controlled to be nearly equilibrium. The structure
of cluster obtained after enough calculation time depended on
the controlled temperature Tc; yielding to graphitic
sheet for Tc < 2600 K, fullerene-like caged
structure for 2600 K < Tc < 3500 K, and
chaotic 3-dimensional structure for Tc >
3500 K. Through the detailed trace of precursors, it was revealed
that the key feature of the formation of the caged structure was
the chaotic 3-dimensional cluster of 40 to 50 atoms which had
large vibrational energy. On the other hand, when the precursors
were kept under lower vibrational energy, the successive growth
of 2-dimensional graphitic structure was observed.

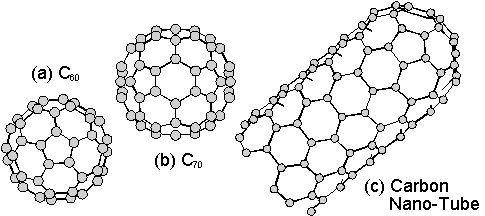
1985年にKrotoら(1)は,黒鉛試料をレーザーで蒸発させ,同時に超音速膨張によって冷却してできる炭素クラスターの質量スペクトルを測定し,原子偶数個のクラスターが卓越していることと,C60のみが極端に多量に観測されること等から,C60の幾何学形状としてサッカーボール型(切頭二十面体: Trancated Icosahidron)の構造[図1(a)]を考え,バックミンスターフラーレン(Buckminsterfullerene)と命名した.その後の量的生成法(2,3),及び単離法(4)の発見により,各種の定量実験が可能となりこの幾何学構造が確定した.一般にC60をバックミンスターフラーレンやバッキーと呼び,C60以外にC70[図1(b)]などの一連のケージ状の炭素クラスターを含めてフラーレンと呼ぶ場合が多い.引き続き,金属をドープしたK3C60結晶の超伝導特性(臨界温度18 K)の発見(5)や,ケージ構造内部に金属を含む金属内包フラーレン(6-8)の量的生成などの話題が次々に現れた.現在も広く物理・化学の分野で基本特性の解明と超伝導特性や半導体特性に着目した全く新しい応用のための研究が国内外で盛んに行われている.
ところが,量的な生成手法(2,3)はいわば偶然に発見されたものであり,その生成メカニズムは依然として明らかとなっていない.現在の実用的なフラーレン生成装置では,数百Torr程度のヘリウムやアルゴンなどの希ガス雰囲気中での黒鉛棒間のアーク放電やレーザー照射によって,10〜15%程度のC60が生成される(2,3,9).一旦は気体となった炭素原子が切頭二十面体という見事な対称性をもつ構造を自発的に形成するという点は驚くべきことである.このような理論的な興味と同時に,C60やC70をさらに大量に効率よく生成する方法や,より大きな高次フラーレン,ナノチューブ[図1(c)]や金属内包フラーレンについてのマクロな量の生成方法を探るためにも,その生成機構を吟味することが重要課題である.
実験的研究によりフラーレンの生成効率が生成環境での緩衝ガスの圧力,温度や流れの影響を強く受け(9),炭素クラスターの冷却過程そのものが重要な因子であることが示唆されている.そこで著者らは比較的長時間に渡る冷却過程を計算可能な分子動力学法によって,フラーレン生成機構の解明に向けた分子シミュレーションの可能性を追っている.既報(10)において一定の条件の下で,不完全ながらフラーレンに近いケージ構造生成の分子動力学シミュレーションが可能であることを示した.本研究では更に,温度,密度などの影響に関して現実の現象との対比を念頭に置き,より合理的なシミュレーションを行い,特に温度の影響について詳細に検討した.
B* : 結合価関数
D : ポテンシャル深さ
Eb : 結合エネルギー
f : カットオフ関数
K : 運動エネルギー
kB : ボルツマン定数
m : 炭素原子質量
N : 全原子数
n : クラスター構成原子数
Rs : 結合変換率
Re : 平衡原子間距離
rij : 原子iと原子j間の距離
r : 位置ベクトル
S : ポテンシャルパラメータ
T : 温度
Tc : 制御温度
t : 時間
VA : 引力項
VR : 斥力項
v : 速度ベクトル
ギリシャ文字
: ポテンシャルパラメータ
: ポテンシャルパラメータ
: クラスターの運動自由度
: 結合間角度
添字
V : 振動運動
R : 回転運動
T :
並進運動
古典分子動力学法を用いて計算を行う上で二つの重要な問題点が指摘できる.一つは炭素原子間ポテンシャルに関するものであり,化学反応を伴うクラスタリング過程をシミュレートする場合,結合状態はsp, sp2, sp3と変化していくため,これらを適切に表現する関数を用いる必要がある.しかしながら,フラーレン生成に適したポテンシャル関数の最適化は本研究の主旨ではないため,ここではBrenner(11)によって提唱された経験的Tersoff(12)型ポテンシャルを簡略化して採用した.
もう一つの恐らくより切実な問題点は,現実の現象との時間スケールの対応である.レーザー蒸発法の実験ではフラーレン形成に要する時間のオーダは100 s程度であると見積もられるが(13),この時間オーダで分子動力学シミュレーションを行うのは,現在の計算機性能では不可能である.そこで本研究では仮想的に炭素原子の密度を圧縮し,衝突頻度を増加させることで時間スケールを短縮することを企てた.このため現象を支配する因子を検討し,密度圧縮に関する影響を補償する必要がある.クラスター成長過程の支配因子を以下の三つの過程,すなわち,
1) クラスター同士の衝突による成長または解離
2) 緩衝ガスとの衝突または熱放射によるクラスターの冷却
3) クラスター同士の衝突後から次の衝突までのクラスター構造のアニール
に大別して考える.仮想的な密度圧縮により1)の衝突回数を増加させていることになる.これを補償するため,必然的に2)の冷却速度を速める必要がある.更に現実の現象では,時間スケールと緩衝ガスの効果を考慮すると,並進,回転,振動の各運動エネルギーが平衡状態になっていると考えられるため,これらを実現した上で冷却を行うべきである.既報(10)では単純な温度補償によって冷却を速める方法を用いたが,この方法ではこれらの運動エネルギーが著しく非平衡となっていた(14).そこで,並進,回転,振動温度を独立に制御することによって,擬似的に平衡状態を実現した.3)の過程に関しては大幅にアニールを抑制したままの状態となっているため,この過程については別個に検討する(15).
2.1 炭素原子間ポテンシャル 炭素原子間相互作用としてBrenner(11)がダイヤモンド薄膜のCVDのシミュレーションに用いたポテンシャルを採用した.これはTersoff(12)の結合価の表記に基づくもので小型の炭化水素,グラファイト,ダイヤモンド構造など多彩な構造を表現出来るよう改良されている.ここで系全体のポテンシャルEbは各原子間の結合エネルギーの総和により次のように表される.

ここでVR(r),VA(r)はそれぞれ反発力項,引力項であり,以下に示すようにカットオフ関数f(r)を含むMorse型の指数関数が用いられている.



B*は結合i-jと隣り合う結合i-kとの角度ijkの関数で,結合状態を表すように引力項の係数となっている.



ここで用いた定数を表1に示す.
Brenner(11)のモデル化では,水素終端されていない小型の炭素クラスターについては考慮されていないが,本研究での前駆体の大部分はこの形状である.このため,このポテンシャルをそのまま用いると小型のクラスターのクラスタリングによる多重環状のネットワーク構造の形成がうまく表されないことが分かった(16).そこで本研究では,共役結合状態に関して炭化水素分子などに最適化されて得られた補正項Fを省略した.
運動方程式の差分にはVerlet法を用い時間刻みを0.5
fsとした.
| De | R2 | |||||
| S | ||||||
| a0 | ||||||
| Re | c0 | |||||
| R1 | d0 | |||||
2.2 温度制御法 原子間距離がカットオフ距離R2よりも短い二つの炭素原子間にC-C結合が存在すると仮定し,C-C結合によって結ばれた炭素原子の集団をクラスターと定義する.n個の炭素原子で構成されるクラスターCnの全運動エネルギーは並進エネルギーKT,回転エネルギーKR,振動エネルギーKVに以下のように分離される.

ここでmは炭素原子の質量,





に対する各構成原子の相対位置,相対速度である.このとき各クラスターの温度,及びそれらに自由度の重みを掛けた系全体の温度(total)はそれぞれ次のように表される.








但し,nは各クラスターの運動自由度,kBはBoltzmann定数である.
先に述べたように平衡状態を実現するため,並進,回転,振動に対して0.1
ps毎に制御温度Tcと各温度の差を60
%に縮小するよう独立に速度スケーリングを施した.
フラーレン生成メカニズムで最も興味深い点は,どのようにしてケージ状の構造が自己形成されるか,また生成過程においてグラファイト,ダイヤモンドとの構造選択の要因が何処にあるかという点である.フラーレン構造の特徴としてその高温安定性が挙げられるが,著者らはそこに構造選択の原因があると考え,高温環境下でのクラスタリング過程を計算し,フラーレン的なケージ構造,及びグラファイト的な平面構造の生成をシミュレートした(10).但し,この計算では単純なスケーリングにより温度制御したため,各温度の平衡状態が実現せず(14),温度,密度などの各パラメータの影響が不明確であった.そこで改めて先に述べた温度制御法を用いた擬似的平衡条件の下で計算を行った.
3.1 クラスター形状の温度依存性 初期条件として200個の炭素原子を全方向に周期境界条件を課した8 nmの立方体中にランダムに配置し,ランダムな方向の速度を与える.その後,並進,回転,振動の各温度を同一の目標温度Tcに制御する.図2はTc = 3000 Kの条件下での時間発展の様子である.20 psではほとんどのクラスターはC3以下の大きさであるが,C10程度のクラスターもいくつかみられる.t = 60 psでは炭素原子数12個程度の鎖状,リング構造のクラスターが成長し,最大のものはC25の多重環状構造をとっている.その後,t = 120 psになると不規則な三次元構造C37, C45, C49と平面構造のC62が現れ,最終的にt = 300 psでは,主に五員環,六員環により構成される閉じた大型のチューブ状の構造C160が得られた.この過程で最初の50 ps程度までは結合によるエネルギーの解放がクラスターサイズに対して極端に大きいため振動温度が高くなるが,それ以降は概ね温度の平衡状態が実現している.

図2の計算と同一の初期条件で制御温度のみを変えて300 ps後に得られた代表的クラスター構造を図3に示す.Tc = 1000 Kでは大型の環状構造を残すものの,ほぼ完全に二次元的な構造をとっている[図3(a)].Tc = 2000 Kになると図3(b)に示すように多重の環状構造によりグラファイト的なネットワーク構造がねじれて繋がった形状となっている.制御温度2600 Kでは大きな穴をもつ不完全ケージ構造が形成され [図3(c)],Tc = 3000 Kでは穴のない中空のケージ構造が観察された[図3(d)].更に高温のTc = 3500 Kの条件下では[図3(e)],規則的な構造を維持することができず四つの結合手を持つ炭素原子を含むランダムな三次元的構造をとる.Tc = 6000 Kになると,熱エネルギーによる解離のため大型の構造を維持することができず単純な構造に移行し,8000 K程度の高温環境下では,クラスターが大きく成長することなく 最大でもC20程度の鎖状,一重のリング構造などの単純な構造をとる.




(a) Tc = 3000 K (b) Tc
= 1000 K
3.2 前駆体の反応過程 前駆体の構造とその振動温度に注目してクラスタリング過程を詳細に検討した. 最終的にケージ構造を形成するTc = 3000 Kの条件でのクラスタリング過程を図4(a)に示す.C20以下の前駆体は基本的に鎖状構造と数個のリングで構成される単純な構造をとっており,これらの衝突によりC40程度の三次元的に不規則な構造をもつクラスターに成長している.そしてその後,(2)で示される過程で激しく結合を変換しケージに近い構造の基礎を作っている.一方C64のクラスターはグラファイト的平面構造をとっている.その後それぞれがクラスタリングし,アニールすることにより閉じたケージ構造を形成している.
図4下部のグラフは上部括弧内の過程に対応するクラスターの振動温度Tv,及び結合変換率Rsを表している.ここでRsは,1 psの間にクラスター内で起こった新規結合と結合切断の回数をクラスターサイズで割ったものである.ここで小型のクラスターは図4(a)の(1)に示すように高い振動温度をもち,激しく結合状態を変え,安定形状を形成することなく成長している.その後図4(a)の(2)の過程に代表されるように,C50程度に成長する過程でアニールし安定構造を模索する.ここで(2)の過程の中程で結合変換率が減少しているが,ここで不安定な鎖状,リング構造から半ケージ状の構造に徐々にアニールしている.
一方,グラファイト的平面構造に成長するTc
= 1000 Kの場合のクラスタリング過程は図4(b)に示すように比較的単純である.この条件では前駆体は常に平面的な構造を形成し,それを二次元方向に拡大するかたちでクラスターが成長していく.この過程全体において各クラスターの振動温度は常に低温に保たれていることが下の図より分かる.またネットワーク構造の変化はクラスター同士の衝突時に衝突部付近でのみ起こり,その部分の形状を整えるようアニールする.
3.3 クラスターサイズ分布の遷移 ここまでの解析によりある温度範囲でケージ構造が選択的に形成されることが示唆されるものの,依然としてC60構造だけが他のフラーレンと比較して選択的に生成されることに関しては何ら説明できない.一般的なアーク放電法により生成されるフラーレンの80 %はC60であるのに対して,レーザー蒸発法で生成されるC60の比率は0.1 %以下である.これはC60の特異性によるものであり,アニールの過程がこの問題の重要な鍵であると考えられる.図4(a)のシミュレーションではC50程度の領域で,余りにも早く次の衝突を迎え,C160にまで成長してしまったため,2章で述べた3)のアニールの過程が極端に短くなっている.ここでアニールの可能な衝突時間間隔について検討するため,クラスター成長の時間履歴に関して考察を加えた.
図5はケージ構造を形成するTc = 3000 Kでのクラスターの成長履歴を示す.ここで縦方向の長い直線は衝突がなく自由にアニールできる時間を示す.三次元的構造をとるクラスターの履歴においては,C40付近で平面構造クラスターにはない非衝突の時間帯があることが分かる.これは,C40程度の領域でクラスターがケージ構造にアニールすることでその衝突断面積が極端に減少するためである.この領域では他のクラスターと衝突することなく十分にアニールするため,ここで完全なフラーレン構造を形成する可能性がある.一旦完全なフラーレン構造を形成すると, 安定化し次の衝突に対して不活性となるため,そのフラーレン構造を維持すると考えられる.このように考えると,最小の安定フラーレン構造であるC60で反応が留まる可能性が最も高く,結果的にC60が選択的に生成されると考えられる.

分子動力学法を用い,高温環境下でランダムに分布する孤立炭素原子のクラスタリングにより不完全ながらフラーレン的ケージ構造を持つクラスターの生成をシミュレートした.また,より低温環境下ではグラファイト的平面構造のクラスターが形成されることが分かった.C50程度の三次元的に不規則,不安定な前駆体がアニールすることで安定なケージ構造が形成されるのに対し,平面的構造は低温で安定状態を保ったまま連続的に二次元構造を拡大していく.また,ケージ構造を形成すると,衝突断面積が減少し,衝突間隔が長くなるため,長時間に渡るアニールが可能となる.完全なフラーレン構造を形成すると,その時点で反応不活性となるためそのサイズに留まると考えられる.
原子間ポテンシャルや時間スケールの圧縮などといった問題が残されているが,孤立炭素原子状態からフラーレン構造をシミュレートしたことにより,フラーレン生成メカニズム解明に向けての有力な足掛かりとなると考えられる.
本研究の遂行に当たり,文部省科学研究費基盤研究07555068,及び特別研究員奨励費08004746の補助を受けた.
(1) Kroto, H. W., ほか4名, Nature, 318-6042 (1985), 162-163.
(2) Krtschmer, W. ほか3名, Nature, 347 (1990), 354-358
(3) Haufler, R. E., ほか7名, Mat. Res. Soc. Symp. Proc., 206 (1991), 627-638.
(4) Taylor, R., ほか3名, J. Chem. Soc. Chem. Communications, 1423 (1990), 1423-1425.
(5) Hebard, A. F., ほか7名, Nature, 350 (1991), 600-601.
(6) Chai, Y., ほか8名, J. Phys. Chem., 95 (1991), 7564-7568.
(7) Shinohara, H., ほか2名, J. Phys. Chem., 96 (1992), 3571-3573.
(8) Kikuchi, K., ほか8名, Chem. Phys. Lett., 216-1,2 (1993), 23-26.
(9) 丸山・ほか3名, 第31回日本伝熱シンポジウム講演論文集 (1994), 943-945.
(10) Maruyama, S. & Yamaguchi, Y., Therm. Sci. & Engng., 3-3 (1995), 105-109.
(11) Brenner, D. W., Phys. Rev. B, 42-15 (1990), 9458-9471.
(12) Tersoff, J., Phys. Rev. Lett., 56-6 (1986), 632-635.
(13) Maruyama, S., ほか2名, Rev. Sci. Instrum., 61-12 (1990), 3686-3693.
(14) 丸山・山口, 第9回フラーレン総合シンポジウム講演要旨集 (1995), 131-133.
(15) 丸山・山口, 機論, "フラーレン生成過程の分子動力学 (第2報,完全なC60へのアニーリング)", 投稿中.
(16) 丸山・山口,
第32回日本伝熱シンポジウム講演論文集
(1995), 839-840.