A Molecular Dynamics Simulation of the Fullerene Formation Process
Yasutaka Yamaguchi and Shigeo Maruyama
Department of Mechanical Engineering, The University of Tokyo,
7-3-1 Hongo, Bunkyo-ku, Tokyo 113, Japan
TEL/FAX: +81-3-5800-6983
e-mail: maruyama [at] photon.t.u-tokyo.ac.jp
Abstract
A molecular dynamics simulation starting from 500 isolated carbon atoms resulted in several closed caged structures under suitable temperature control. A caged C70 cluster that appeared in the simulation was traced back to study the dynamics and the structure of Cn precursors: simple chain and ring for n<20, tangled poly-cyclic structure for 20<n<30, and random caged structure for n>30. Furthermore, it was found that the final caged structure was obtained when the control temperature was roughly in the range from 2500K to 3000K, and a graphitic flat structure resulted in lower control temperatures.
1. Introduction
In 1985, the existence of soccer-ball structured C60 was demonstrated by Kroto et al. [1] through their time-of-flight mass spectra of carbon clusters generated by the laser-vaporization supersonic-nozzle technique. Later, the discoveries of simple techniques for macroscopic generation and isolation of fullerene in 1990 [2-4] made this new material ready for applications in many fields. Furthermore, the observation of superconductivity by Hebard et al. [5] at Tc=18 K of potassium-doped C60 crystal gave a further motivation to the research field. Within a few years, macroscale amounts of metal containing fullerenes [6,7], higher fullerenes and carbon nanotubes [8] were available. Recently, high quality bulk generation of single wall nanotubes (SWNT) is an exciting prospect [9].
Although fullerene is now recognized as an attractive new material and many reports regarding applications have been proposed, the mechanism of how such a symmetric hollow caged structure can be self assembled is still unknown; the technique of fullerene generation was indeed discovered almost accidentally. Besides theoretical physical interests, it is important to know the formation mechanism in order to find the optimum conditions for synthesizing metal containing fullerene, higher fullerene, and SWNT. Here we have performed molecular dynamics simulations to investigate the mechanism of empty fullerene formation.
Several groups have approached the formation mechanism using molecular simulations. Chelikowsky [10] calculated the rapid cooling process of 60 isolated carbon atoms by using the molecular dynamics method. Although he demonstrated the formation of a C60 caged structure, his results seemed to depend greatly on an unrealistic high-density condition. Another simulation used a graphitic sheet as the initial condition [11], and showed merely the curling of the sheet. Schweigert et al. [12] simulated the formation of C60 caged clusters from the C60 tri-cyclic rings proposed by Helden et al. [13,14] by using the Monte-Carlo method, and Astakhova et al. [15] simulated the formation process of a small caged structure by using the tight-binding molecular dynamics method. However, all of these simulations enforced particular boundary conditions or initial conditions in order to make the caged structures. Furthermore, as far as we know, no simulation has been able to achieve a perfect fullerene structure. Here, we demonstrate simulations without an artificial constraint which serves to guarantee the formation of the caged structure. And, this result leads to the demonstration of the formation of perfect Ih C60 structure, as detailed in another paper [16].
2. Numerical Technique
There were two major difficulties in simulating the process of fullerene formation by molecular dynamics method. One was the potential function; in order to simulate a system including chemical reactions, an appropriate potential function was required to handle the variable bonding states including sp, sp2 and sp3. We applied the empirical potential function proposed by Brenner [17], which was based on Tersoff’s [18] bond-order expression and optimized for small hydrocarbons, graphite, and diamond crystal. The process of clustering from small clusters to poly-cyclic structures could not be simulated in our preliminary simulations [19], probably because non-terminated small carbon clusters were not taken into account in Brenner's modeling. In order to avoid this problem, we ignored the conjugate-compensation term F in his original expression [see Appendix I for more details]. The simple Verlet’s method was adopted to integrate the equation of motion with the time step of 0.5 fs.
The second and more severe problem was the time scale of the phenomena. The order of time for fullerene formation through the laser irradiation or arc-discharge method was roughly estimated to be from 1 ms to several seconds, so simulating the whole process by present computers was hardly realistic. We therefore tried to compress the time by increasing the number density of carbon atoms. The effects of compression involve three processes: 1) the growth or dissociation of clusters due to collisions, 2) the cooling process through collisions with buffer gas or radiation, 3) rearrangements of the network structure during the annealing process between collisions. The density compression enhanced the first process. By giving a rapid cooling rate, the effects on second process, cooling, could be compensated for. Considering the effect of the buffer gas, the equilibrium of translational, rotational, and vibrational temperatures were enforced in order to mimic the longer time scale phenomena [see Appendix II]. Finally, the lack of the annealing was evaluated in another report [16].
3. Simulation Results
3-1. Formation of Caged Structure
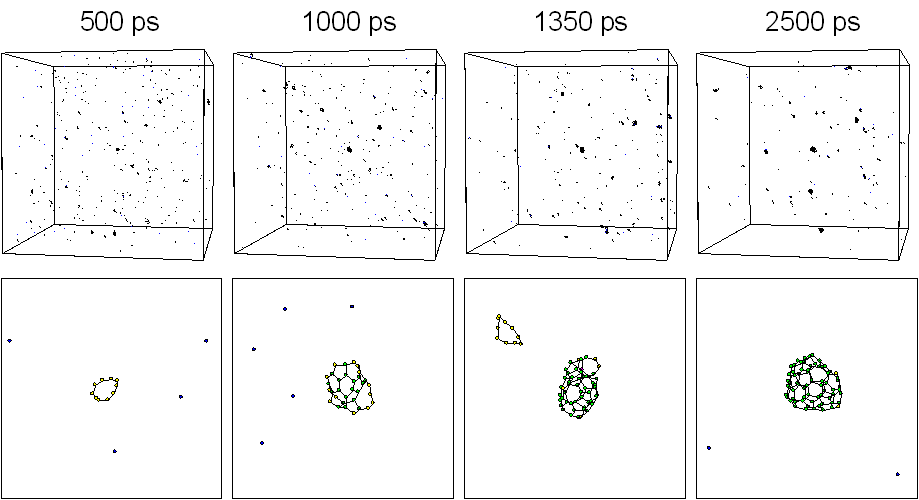
Five hundred carbon atoms in gas phase with random positions and velocities were distributed in a 342 ƒi cubic box with full periodic boundary condition. The system was controlled toward a control temperature Tc of 3000 K. Fig. 1 shows typical snapshots of the clustering process. Motion pictures are available at our WWW site [20]. At 500 ps, some clusters formed chain or ring structure around C10 and many carbon atoms were in forms of isolated atom, dimers, and trimers. A zoom up picture of a 10 membered ring is shown in the bottom panel. At t=1000 ps, one of the largest cluster grew to about C30 size range. At 1350 ps, a C52 cluster of almost closed caged structure appeared as shown in the bottom panel. Finally at 2500 ps, the largest cluster had grown to C70 with an almost closed caged structure and there was another spherical C58 cluster.
Fig. 1. Snapshots of the clustering process for Tc = 3000 K.
Fig. 2 shows the growth of the C70 cluster after 2500 ps in the simulation. The vertical position and horizontal length denote the size and the duration of existence of clusters, respectively. For example, the C60 and C8 clusters existed independently from about 1900 ps to 2000 ps, coalesced at 2000 ps, and then, they grew to C69 and C70 with additions of two other atoms at about 2100 ps and 2130 ps. Here the histories of clusters smaller than C8 were omitted. Small clusters up to C20 formed simple structures like chains or rings. These simple structures grew to tangled poly-cyclic structures around C20; these clusters did not keep any fixed stable structures and indeed, there were frequent rearrangements of the network structures. Then the cluster grew larger from C30 through C60, gradually attaining a random caged structure. The number of carbon atoms was not enough to form a complete closed cage until around C60, when a hollow caged structure like fullerene first appeared.
Comparing the lifetime of each cluster, C60 and C70 stayed at the same sizes for relatively long times due to their small collisional cross section. These caged clusters could have annealed to more sophisticated structures during these intervals. This annealing effect was considered in a separate paper [16].
Fig. 2. A dynamic path to a caged cluster C70.
3-2. Effect of Temperature Control
One of the most important questions in the fullerene formation is that of in which conditions the fullerene is preferable to graphite or diamond structures. From experimental observations, relatively high temperature is expected to be the key for the fullerene formation. Here, we investigated the influence of the control temperature on the final structure of clusters. In order to perform many runs at various temperatures, we used a smaller simulation system of 200 atoms in a cubic box of 80 ƒi.
Fig. 3 shows the largest clusters obtained at t=300 ps at various temperature conditions. At Tc=1000 K, the cluster had an almost 2-dimensional flat structure which anneals to the graphitic sheet [Fig. 3(a)]. At Tc=2000 K, the cluster was made of two flat structures merged together [Fig. 3(b)]. At Tc=2600 K and Tc=3000 K, imperfect hollow caged structures were observed [Fig. 3(c,d)]. For higher temperature around Tc=3500 K, the cluster had a random bulky structure including some carbon atoms with 4 bonds in the middle of the sphere [Fig. 3(e)]. At Tc=6000 K, large clusters preferred to have curled long chain structures and thermal dissociation had an important role [Fig. 3(f)]. When the control temperature was as high as 8000 K, there were only chains and rings smaller than C20. Thermal dissociation prevented the clusters from further growth, and entropy ruled [Fig. 3(g)].
Fig. 3. Structures of clusters obtained with various control temperatures Tc
The dynamic process leading to the caged structure (Tc=3000 K) can be compared with the process leading to the graphitic sheet as shown in Fig. 4. The precursor clusters in the reaction process were observed in detail with a special attention to the structure and the vibrational temperature. When Tc=3000 K, the cluster growth process was similar to the case shown in Fig. 2. The bottom panel of Fig. 4(a) shows the local vibrational temperature TV and the bond-switching rate Rs during typical transformations. Here, the bond-switching rate Rs of a cluster Cn was defined as the number of bond creations and breakages in a cluster in 1 ps divided by n. The initial high vibrational temperature was caused by the release of potential due to coalescence of small clusters. Even though the control temperature was set at 3000 K, the vibrational temperature rose up as high as 5000 K when small chains and rings frequently merged each other. This initial high temperature activated the formation of the random caged structure as seen in process (2). After this process, the vibrational temperature was kept at about 3000 K. Even during a collision of larger clusters as in (3) and (4), the temperature rise was relatively small due to a large number of degrees of vibrational freedom.
On the other hand, the clustering process at Tc=1000 K [Fig. 4(b)], yielding the flat structure was quite simple. Because of the high cooling rate, the initial temperature rise was only up to 2000 K, which was not enough to activate transformations from the flat structure. Hence, the cluster simply extended the flat structure in the 2-dimensional direction by successive coalescence at side edges.
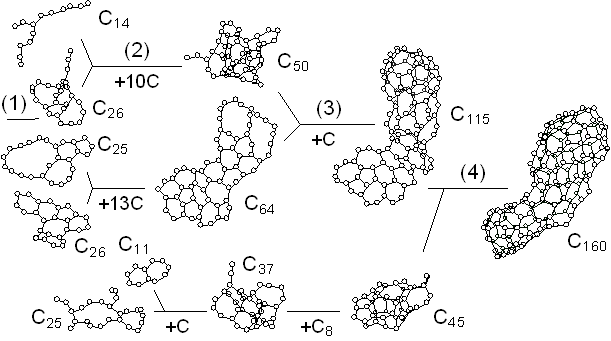
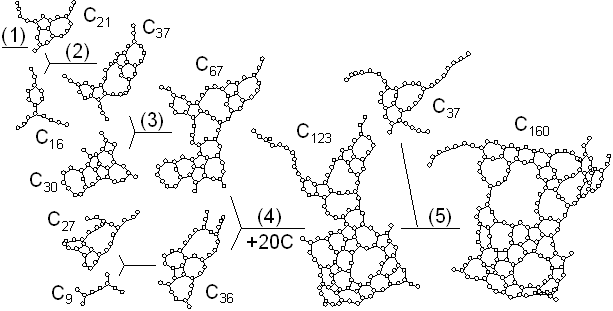
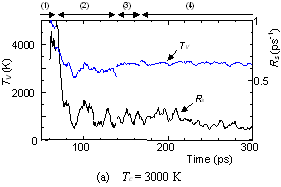
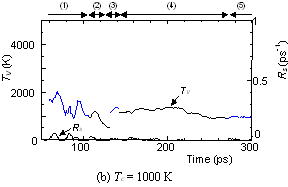
Fig. 4. Vibrational temperature of precursors in the clustering process. Parenthesized numbers in top and bottom panels correspond.
4. Conclusion
By using the molecular dynamics method, the process of fullerene-like caged cluster formation was demonstrated from gas phase carbon atoms. A dynamic reaction process leading to a C70 cluster was analyzed. The typical structure of small precursors Cn was chain for n<10, and ring for 10<n<20. When the appropriate temperature control (cooling rate) was applied, the potential release due to the coalescence of small pieces gave very high vibrational temperature at about C20. This increase in the temperature activated the transformation from flat structures to tangled poly-cyclic structures. These clusters became the seeds for the caged fullerene-like structures after further addition of small pieces and annealing. The dependence of the final structure on temperature was studied with smaller simulation systems. It was found that the fullerene-like caged structure was obtained when the control temperature was roughly in the range of 2500 to 3000 K, and the graphitic sheet structure was obtained for lower temperature.
Acknowledgements
This work was supported by a Grant-in-Aid for Scientific Research (B) and a Grant-in-Aid for JSPS Fellows from the Ministry of Education, Science, Sports and Culture, Japan.
References
Appendix I. Potential Energy Expression
The total energy of the system Eb was expressed as the sum of the bonding energies between all atoms i and j.
![]() (1)
(1)
where VR(r) and VA(r) were repulsive and attractive force terms, respectively. Morse-type exponential functions with a cut-off function f(r) were used for these terms.
![]() (2)
(2)
![]() (3)
(3)
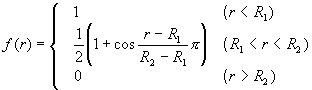 (4)
(4)
The bonding state was described through the term B* as the function of the angle q ijk between bond i-j and each neighboring bond i-k.
![]() ,
,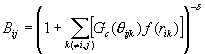 (5)
(5)
where
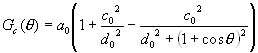 (6)
(6)
Constants used are summarized in Table 1.
Table 1. Potential Parameters
De (eV) S b Re (ƒi) R1 (ƒi) 6.325 1.29 1.5 1.315 1.7 R2 (ƒi) d a0 c0 d0 2.0 0.80469 0.011304 19 2.5
Appendix II. Temperature Control
A pair of carbon atoms closer than the cut-off distance R2 with each other was considered to share a bond, and a group of carbon atoms connected with bonds were defined as a cluster. The total kinetic energy of the cluster Cn containing n carbon atoms was separated into translational, rotational and vibrational energy, KT, KR, KV, respectively.
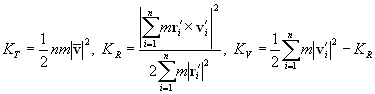 (7)
(7)
where m denoted the mass of carbon atom, and
![]() ,
,![]() were position and velocity relative to those of the center of mass of the cluster
were position and velocity relative to those of the center of mass of the cluster
![]() ,
,![]() .
.
The temperatures of each cluster, TT, TR, TV, and the total temperatures TTt, TRt, TVt were expressed as follows.
![]() ,
, ![]() (8)
(8)
![]() ,
, ![]() (9)
(9)
![]() ,
, ![]() (10)
(10)
where n and kB were the number of degrees of freedom of motion and Boltzmann's constant, respectively. In order to enforce temperature equilibrium, each temperature of the system was independently controlled to the control temperature Tc so that the difference between TT,R,V and Tc was reduced by 60 % in 0.1 ps.