沸騰熱伝達の数値シミュレーションの試み
A Numerical Simulation of Boiling Heat Transfer
丸山
茂夫,賀 纓,庄司 正弘
Shigeo Maruyama, Ying HE and Masahiro SHOJI
Dept. of Mech. Engng., The University of Tokyo, 7-3-1 Hongo, Bunkyo-ku, Tokyo
This paper reports a method to simulate heat transfer from boiling surface by using time dependent dry-patterns of the macro-layer. Employing a one-dimensional heat conduction model, the processes of heat transfer for nucleate boiling, critical heat flux condition, and transition boiling were simulated. In addition, equivalent thickness of macro-layer, heat flux, and the surface wettability effect were predicted. The simulated results agree well with the experimental data. It is suggested that the numerical simulation is useful in understanding the mechanism of boiling heat transfer more clearly.
Key Words
: Boiling Heat Transfer, Numerical Simulation, Macro-Layer, Transition Boiling, Critical Heat Flux
1.はじめに
限界熱流束を含む高熱流束核沸騰から遷移沸騰の熱伝達において,合体気泡下のマクロ液膜の蒸発が重要な意味を持つとされているが
(1),合体気泡の生成から離脱の間に,マクロ液膜がどのように蒸発していくものであるか,すなわち加熱面の乾きが時間的,空間的にどの様に変化するものであるかについてはあまり明らかにされていない.そこで著者らはマクロ液膜の乾きパターンと熱流束の時間進展のシミュレーションを行い,マクロ液膜の変化の様子を視覚的に理解するとともに,甲藤ら(1)の空間平均的な考え方,Dhirら(2)の時間平均的な考え方との比較を行ってきた(3-6).合体気泡の離脱直後のマクロ液膜厚さと乾き率を仮定することにより,沸騰曲線の傾向,合体気泡の成長速度(5),空間平均乾き率(5),接触角の影響(5,6)をシミュレートできることを示した.本報では,このシミュレーション手法についての解説と今後の展望について述べる.

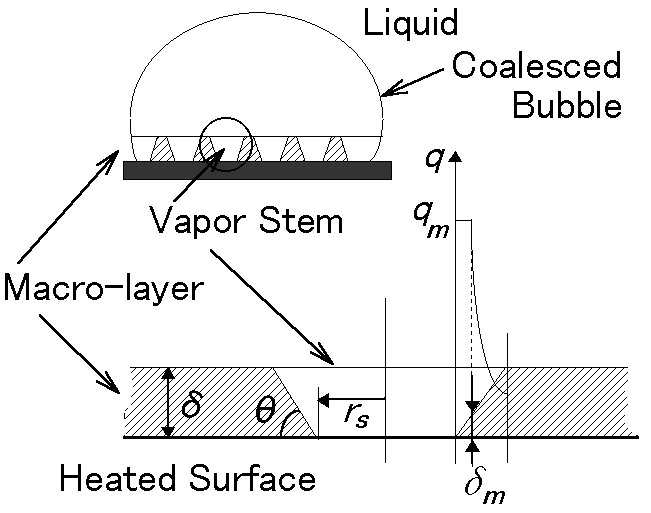
Fig. 1 Model of heat conduction and evaporation
2.数値シミュレーション手法
数値シミュレーション手法は,若干の改良はあるものの前報
(3-6)でほぼ共通である.合体気泡が離脱した後に直ちに新しい合体気泡が生成され,その元に一定量の液が取り残されると考え,この瞬間(時間t = 0)からの液の蒸発を考える.初期状態としては,壁面加熱度に応じて実験的に求められた初期液膜厚さd 0,初期ボイド率a 0のマクロ液膜を仮定する.初期の乾きパターンはランダムな位置にランダムな大きさの円形蒸気ステム(初期半径最大値rmax以下との拘束条件を付ける)が存在するとする.時間進行は,液膜厚さd (t)の減少と蒸気ステム半径rs(t)の増大をそれぞれ独立に以下の簡単なモデルに基づいて計算する.すなわち,液膜の蒸発による厚さ変化は縦方向一次元熱伝導で近似される熱流束が蒸発潜熱と釣り合うと考え,以下の式より求める.
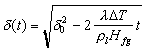 (1)
(1)
ここで,l
: 液の熱伝導率, r l: 液の密度, Hfg:: 蒸発潜熱, D T: 壁面過熱度である.一方,蒸気ステム半径の成長速度drs/dtは,Fig. 1のようにモデル化した蒸気ステムと液膜の接触面が一定の角度q を持つと考えたときの斜面での蒸発量を縦方向一次元熱伝導で評価される熱流束と釣り合うとして求め,液膜の接触角q が常に一定であるとの拘束条件を仮定すると,以下の式で計算される.
 (2)
(2)
ここで,d
mは気液固体面の三相界線での熱流束が無限大となるのを避けるために導入した熱流束の上限値(8)



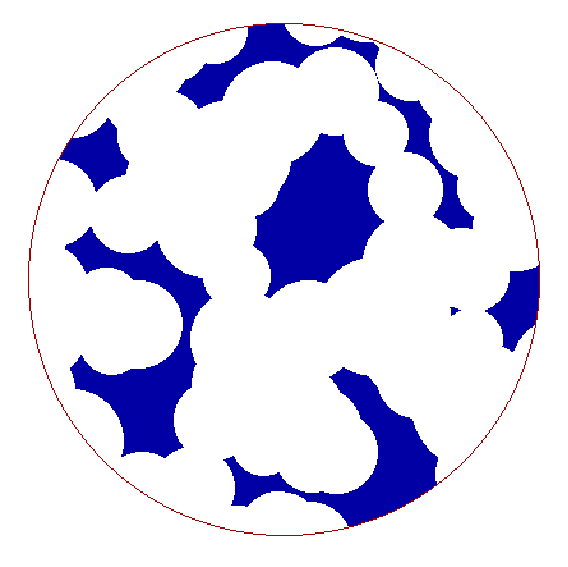
(a) t = 0 ms (b) t =15 ms (c) t = 24.5 ms (d) t = 37 ms
a
= 10 % a = 35 % a = 55 % a = 79 %d
= 33 m m d = 29 m m d = 27 m m d = 23 m mFig. 2 Periodic change of dry patterns on 10 mm diameter heated surface near CHF condition of D T = 23K &
3.乾きパターン・液膜厚さ・熱流束の時間変化
Fig. 2
に計算された乾きパターンの一例を示す.大気圧・飽和水の限界熱流束状態を想定し,D T = 23 K,d 0 = 33 m m,a 0 = 10 %とした場合である.さらに,後述の沸騰曲線が庄司らの実験(7)と合うようにq = 6゜,rmax = 0.4 mmとした.黒い部分が液膜,白い円形部が蒸気ステムを表す.Fig. 3にはボイド率a の時間変化とともにマクロ液膜厚さd の変化,全液量等価厚さW=d (1 - a )及び熱流束qをプロットした.ここで,熱流束qは,乾き面からの伝熱は無視して,以下の式のように液膜厚さの減少に対応する熱流束qsと蒸気ステムの成長に対応する熱流束
qa に分離して考えられる.
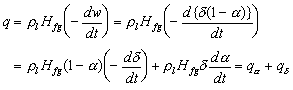
Fig.3
において特徴的なのは,qa の影響で熱流束qが時間とともに増加し一旦最大値をもって減少する点である.これは,Fig.2の乾きパターンから直感的に分かるように,ボイド率の変化に伴って,最も蒸発の盛んな蒸気・液界面長さ(蒸気ステムの濡れぶち長さ)がa =0.4〜0.5の時に最大値を持つからである.また,ボイド率が大きくなると液膜中にステムがあるというよりは,沸騰面上に液滴が残っていると考えられるパターンに変わっていく[Fig.2(d)].Fig.2に示す結果の場合は,71ms後にd ¹ 0で乾ききり,液膜厚さの減少の効果より蒸気ステムの成長の効果がわずかに強く現れている.一方,D Tを大きくするかd 0を小さくすると厚さの減少の効果がより強く現れ,乾ききるまでの時間は式(1)より
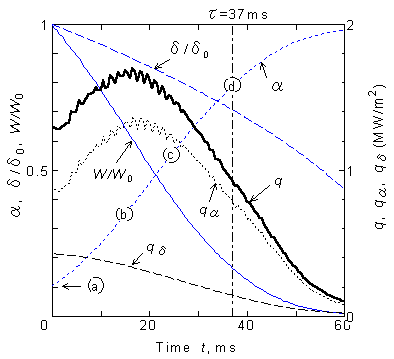
Fig. 3 Change of heat flux q by void fraction a and thickness d for near CHF condition
4.沸騰曲線
壁面過熱度D
Tを変えたときの初期液膜厚さd 0の変化として庄司ら(7)の観察を採用し,初期ボイド率は庄司ら(7)の結果とGaertnerら(9)の結果に基づき10%で一定と仮定する.庄司ら(7)はd 0を熱流束に対して整理しているので,核沸騰の沸騰曲線相関式と遷移沸騰域の瞬間最大熱流束の包絡線(10)を組み合わせて過熱度に対する厚さを求めた(5).これらの条件下で,q とrmaxを最適化して得られた沸騰曲線がFig.4である(q = 6゜, rmax = 0.4mm).ここで,気泡離脱周期t は庄司ら(7)の結果によって遷移沸騰域ではわずかに増大するものの簡単のために37msで一定とした.さて,Fig.4には仮定したd 0, a 0, t より定まる平均熱流束の上限値
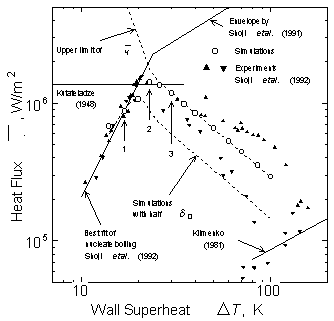
Fig. 4 Simulated boiling curves
5.空間平均的モデルと時間平均的モデル
シミュレーションの結果より,周期t
= 37 msで合体気泡の離脱を繰り返すとして熱流束と全液量等価液膜厚さW = d (1 (1 a )の時間変化を示したのがFig.5である.この場合には,初期乾きパターンを決定する乱数を各周期で変えてみたが,各周期ごとの差異は僅かである.甲藤ら(1)は,高熱流束核沸騰のときにはマクロ液膜が乾くより前に合体気泡の離脱(液の供給)が起こるが,限界熱流束条件下では,液膜が乾ききると同時に液の供給があり,さらに液膜が乾いてから液の供給までの間に伝熱劣化があると遷移沸騰となると考えた.Fig.5は,CHF状態において必ずしも完全に乾ききらないという点を除けばこの考えを裏付けている.若干の修正は,Fig. 3より明らかなように,一定値以上のボイド率となると熱流束が極端に減少するため,この減少が小さいうちに液の供給があるときに最大の平均熱流束が得られることによる.Fig.6
には,計算された時間平均のボイド率を庄司ら(7)とDhirら(2)の実験結果と比較して示す.時間平均ボイド率は,核沸騰域では設定した初期ボイド率とさほど変わらないが,CHF点近傍で急激に大きくなり,遷移沸騰域では周期と比べて極短期間で乾ききってしまうので1に近づく.庄司ら(4)の結果は,液膜計測針の有限の大きさのために,膜沸騰においても壁面ボイド率が80%程度と小さく見積もられることを考慮すると実験とシミュレーションはよく一致している.さて,
Dhirら(2)は,このマクロ液膜の時間平均ボイド率が接触角によって異なることに基づき時間平均的乾きパターンをモデル化し,接触角による沸騰曲線の変化を予測した.本シミュレーションの結果は彼らの実験結果(f = 14゜)に近い結果を与え,さらに,沸騰面の接触角が増加するとd 0が減少すると考えると(11),Fig. 6のd 0を半分とした計算は接触角の増大と対応し,彼らの実験結果と符合する.接触角の影響は,初期液膜厚さに強く現れると考えられるが,これと同時に蒸気ステムの成長にも影響すると考えられる.この点に関しては,初期液膜厚さはとりあえず一定としておいて,単純に本モデルで用いている接触角q を変化されると定性的には限界熱流束に対する接触角の影響を測定した既存の実験データをよく再現する
(6).恐らく,現実には接触角を変化させると,初期液膜厚さと蒸気ステムの成長速度の両者が熱伝達に影響すると考えられる.
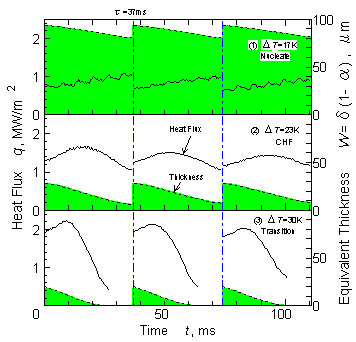
Fig. 5 Periodic change of heat flux and equivalent thickness of macro-layer for (1) Nucleate (2) CHF (3) Transition boiling regimes
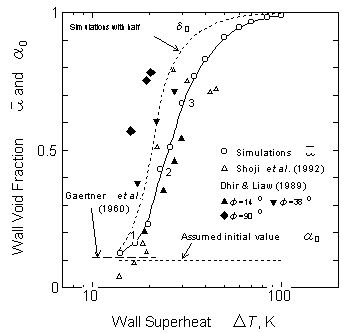
Fig. 6 Time averaged wall void fraction
6.
終わりに本シミュレーションによってマクロ液膜の概念を空間的にも時間的にも平均化しない形でのモデル化ができ,乾きパターンの時間変化から,最も効率の良い熱伝達が可能な三相界面の長さ変化によって沸騰曲線に特徴的な高熱流束核沸騰,限界熱流束から遷移沸騰へと至る特徴を表現できた.さらに定量的な議論を行うためには,正確な初期液膜厚さと初期乾き率,合体気泡の離脱周期などの見積が必要である.これらのパラメータを自立的に決定できないところにシミュレーションとしての限界があると考えられる.
特に,熱流束の絶対値はこれらの条件の与え方に強く依存することが明らかである.ここで,最も切実な問題はマクロ液膜の厚さや乾き率が決定されるメカニズムが不明な点である.液の補給が合体液膜の離脱によって起こると素直に考えれば,このときに誘起される液の流れが重要な意味を持つと考えられるし,壁面近傍の加熱液中での核生成も乾き率や液膜の形状に強く影響すると考えられる.これらの複合的な問題を一つずつ解明する必要があると考えられる.
さらに,本シミュレーションで仮定した蒸発のモデルの妥当性は,高温下での固液の接触の挙動の理解に強く依存する.著者らの簡単な分子動力学法による計算によって
(12)沸点以上の高温壁面に接触する液滴はかなり小さめの接触角を持つと考えられる予備的な結果が得られている.このような物理的な現象の解明が急がれる.
参考文献
(1)
甲藤・横谷,機論34-258(昭43), 345.(2) V. K. Dhir and S. P. Liaw, Trans. ASME, J. Heat
Transfer 111(1989), 739.(3)
清水・丸山・庄司,熱工学講演会910-84(平3), 85.(4)
丸山・庄司・清水,第29回日本伝熱シンポ(平成4), 303.(5) S. Maruyama, M. Shoji, and S. Shimizu, 2nd JSME-KSME Thermal Engng. Conf. (1992), 3.345.
(6) Y. HE, M. Shoji and S. Maruyama, “Numerical Simulation of Boiling Heat Transfer,”
日本機械学会74期総会講演会, International Session.(7)
庄司・黄・田中・横谷,第29回伝熱シンポ(平4),F161.(8)
庄司,日本伝熱研究会第2回トピカルワークショップ(平2),66.(9) R. F. Gaertner and J. W. Westwater, Chem. Engng.
Prog. Symp. Ser. 56-30(1960), 39.(10) M. Shoji et al., 3rd ASME-JSME Therm. Engng. Joint
Conference 2 (1991), 333.(11)
庄司・黒木・徳増,第29回伝熱シンポ(平4), 432.(12)
丸山・倉重・山口,”固体面上の液滴の非平衡分子動力学シミュレーション,” 第34回伝熱シンポ(平9).