Chirality and symmetry of
Nanotube
By wrapping a hexagonal sheet with certain cut, geometry of nanotube can be reproduced.
Several examples are as follows.
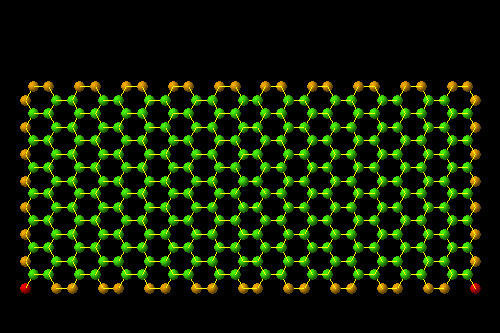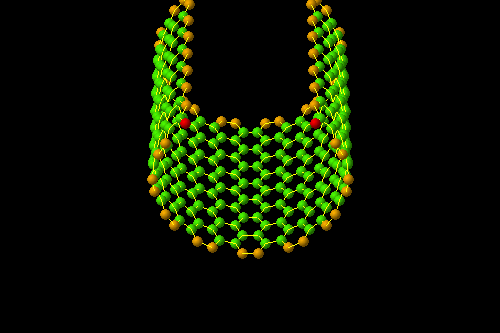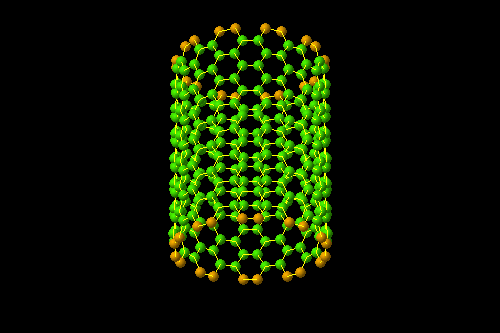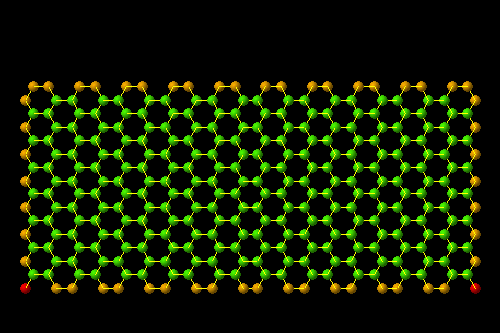 (10,10)
(10,10)
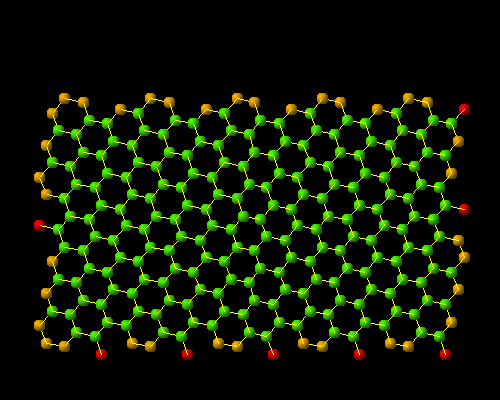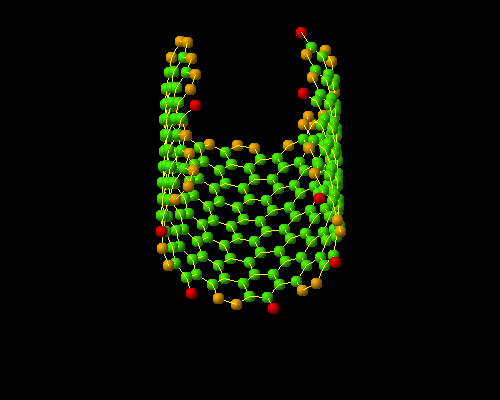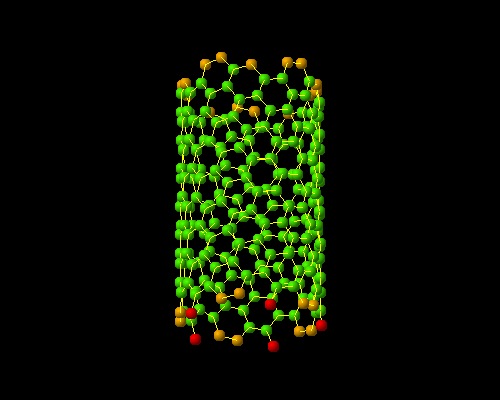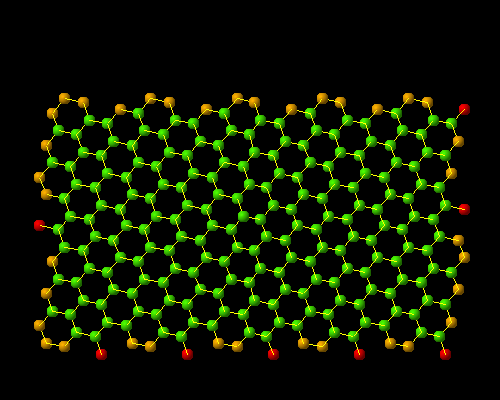 (10,5)
(10,5)
Hence, the geometry of nanotube (except for cap region on both ends) can be uniquely determined by the chiral vector of original hexagonal lattice.
Definition of chiral vectors in the hexagonal lattice is

Chiral vector is defined as ![]() using the
vectors a1 and a2 for the hexagonal
lattice. Note that for the hexagonal lattice a unit cell is made of 2 atoms.
Note also depending on textbook, a1 and a2
are defined as 2 vectors with 120 deg. openings.
using the
vectors a1 and a2 for the hexagonal
lattice. Note that for the hexagonal lattice a unit cell is made of 2 atoms.
Note also depending on textbook, a1 and a2
are defined as 2 vectors with 120 deg. openings.
With this definition in the figure a1 and a2 can be expressed using the Cartesian coordinate (x, y).
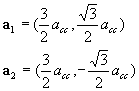
Here, ac-c is the bond length of carbon atoms. For graphite ac-c = 1.421 Å. This same value is often used for nanotubes. But, probably, ac-c = 1.44 Å is a better approximation for nanotubes. It should really depend on the curvature of the tube. A slightly larger value for more curvature is known.
Since the length of a1, a2
are both ![]() , this a is the unit length. Hence,
, this a is the unit length. Hence,
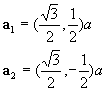
Length of the Chiral vector Ch is the peripheral length of the nanotube:
![]()
For Armchair nanotube
(m = n): ![]()
Further
examples, for (5,5): ![]() , for (10,10):
, for (10,10): ![]()
For zigzag nanotubes
(m = 0): ![]()
Further
examples, for (10,0): ![]() , for (16,0):
, for (16,0): ![]()
Hence, the diameter of nanotube dt is
![]()
For
armchair (n=m):![]()
For
zigzag (m = 0): ![]()
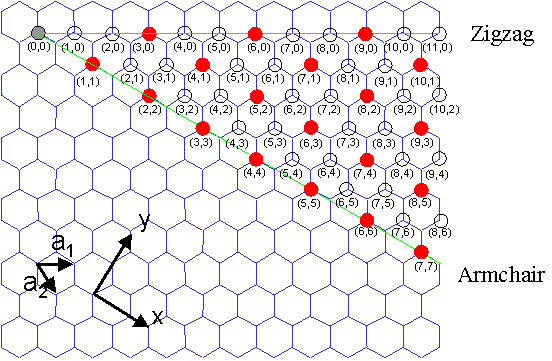
Possible choice of n and m is explained in the following figure.
From R. Saito, M. Fujita, G. Dresselhaus, and M. S. Dresselhaus, Electronic Structure of Chiral Graphene Tubules, Appl. Phys. Lett. 60 (18), 1992.
Here, a red solid point represents metallic nanotube and a black open circle represents semiconductor nanotubes. The condition for the metallic nanotube is: 2n+m=3q (q: integer), or (n-m)/3 is integer.
The unit lattice vector (translational vector) T, perpendicular to the chiral vector is expressed as
![]()
The length T is the unit lattice length along the tube axis direction.
![]()
Here,
![]()
and d is the highest common divisor of (n,m).
For
armchair (m=n): ![]() ,
,![]()
Then, ![]()
For
zigzag (m=0): ![]() ,
, ![]()
The Chiral angle q (angle between the chiral vector and the zigzag direction) is defined as
![]()
Armchair
m = n: ![]()
For
chiral tubes: ![]()
Number of hexagons in a unit cell N is
![]()
Armchair
m = n: ![]()
Zigzag
m = 0: ![]()
For tables of those value up to (40,40)
nanotubes, click here.