A Molecular Dynamics Demonstration of Annealing to a Perfect C60 Structure
Shigeo Maruyama
and Yasutaka YamaguchiDepartment of Mechanical Engineering, The University of Tokyo,
7-3-1 Hongo, Bunkyo-ku, Tokyo 113, Japan
TEL/FAX: +81-3-5800-6983
e-mail: maruyama@photon.t.u-tokyo.ac.jp
Abstract
The formation process of imperfect fullerenes C60 and C70 was simulated using the molecular dynamics method as described in our previous report. These imperfect fullerenes were kept at 2500 K to evaluate annealing effects. Through successive Stone-Wales transformations, perfect fullerene structures were achieved both for C60 and C70 in about 200 ns. The annealing temperature and time scale were plausible, compared to experimental conditions as seen in an Arrehenius plot. Similar simulations were performed for smaller clusters at each stage of the clustering process. Based on these simulations, a fullerene formation model is proposed.
1. Introduction
After the discovery of the macroscopic generation [1,2] and isolation techniques of fullerene, we can produce certain amounts of fullerene by following certain technical procedures. However, many questions are still unresolved such as why the energetically less stable C60 structure is preferred to graphite or larger fullerenes, and why the extracted higher fullerenes show the magic numbers. Furthermore, although the macroscopic generation of metal containing fullerenes [3], carbon nanotubes [4], or high quality single wall carbon nanotubes (SWNT) [5] are now possible, the mechanisms of the selection of certain morphologies are not understood. As well as its intrinsic interest, consideration of the formation mechanism will be crucial for further optimization of these techniques and for the generation of newer morphologies.
Proposed models for the formation mechanism of empty fullerene can be roughly divided into two major concepts: “pentagon road” and “fullerene road.” The “pentagon road” model, proposed by Haufler et al. [2], proposed that additions of pentagonal rings into the hexagonal network were the primary reason for curvature leading to a spherical structure. They argued that the inclusion of pentagonal rings had the advantage of reducing the number of dangling bonds. In addition, they suggested that it was unlikely to have two pentagons next to each other because they would induce too much stress: this is known as the Isolated Pentagon Rule (IPR). Wakabayashi & Achiba [6] suggested a similar model where fullerene was constructed by the stacking of proper sized carbon rings. They explained the magic numbers of higher fullerene [7,8] and the observed ratio of isomers of C76, C84 and C86 [9] with their model.
Heath [10] proposed “fullerene road” model that clusters grew as linear chains up to C10, rings for C10 to C20, and fullerene from about C30, with successive C2 additions at the point of two neighboring pentagons followed until the satisfaction of IPR: this was the reverse of the process seen in laser dissociation experiments.
Helden et al. [11,12] showed using the ion-chromatography that the isomer structure of C60+, double-cyclic or triple-cyclic ring, annealed to fullerene C60 under high temperature conditions, and suggested these structures as the precursors of fullerene. According to their model, the lanthanum-containing fullerene was also formed from a similar double ring structure La(C60) through a transformation [13].
Other models have considered many other kinds of precursors such as a single long chain [14], a piece of graphite sheet [15], or a fragment of carbon nanotube [16].
Experimental results using a mixture of 12C and 13C isotopes showed that the graphite source material was at one stage decomposed into small pieces such as atoms, dimers or trimers [17-19]. In contrast, another experimental result using naphthalene as the combustion resource showed possible effects of the addition of 10-carbon naphthalene-derived units in the ratio of production of fullerene varieties [20], that meant the complete decomposition itself was not an inevitable process.
We have performed molecular dynamics simulations of the clustering process of carbon atoms to examine the formation mechanism. The temperature dependence of the cluster structures was observed in our previous report [21]; graphite-like structures resulted when the control temperature Tc was lower than 2500 K, fullerene-like caged structures for 2500 K<Tc <3500 K, and chaotic 3-dimensional structures for Tc>3500 K. In addition, we simulated the clustering process under a lower density condition at Tc=3000 K in order to give longer collision free time – although much shorter than that in practice –, and obtained C60 and C70 clusters with sophisticated hollow caged structures. In this paper, we explore the possibility of rearrangements into the perfect fullerene structure given sufficient collision-free annealing time, and examine the preferred structures of precursor clusters by the same method. Based on these results, we present a new model of fullerene formation.
2. Numerical Techniques
The Brenner type [22] potential function between carbon atoms used was the same as in our previous report [21]. The temperature control method was also similar, but only rotational and vibrational temperatures were controlled toward a control temperature, since we deal with an isolated cluster in this report. The same rate of temperature control was applied: the difference between current and control temperature Tc was reduced by 60% every 0.1 ps. Verlet’s method was adopted to integrate the equation of motion.
3. Results
3-1. Annealing to Perfect C60 and C70 Structures
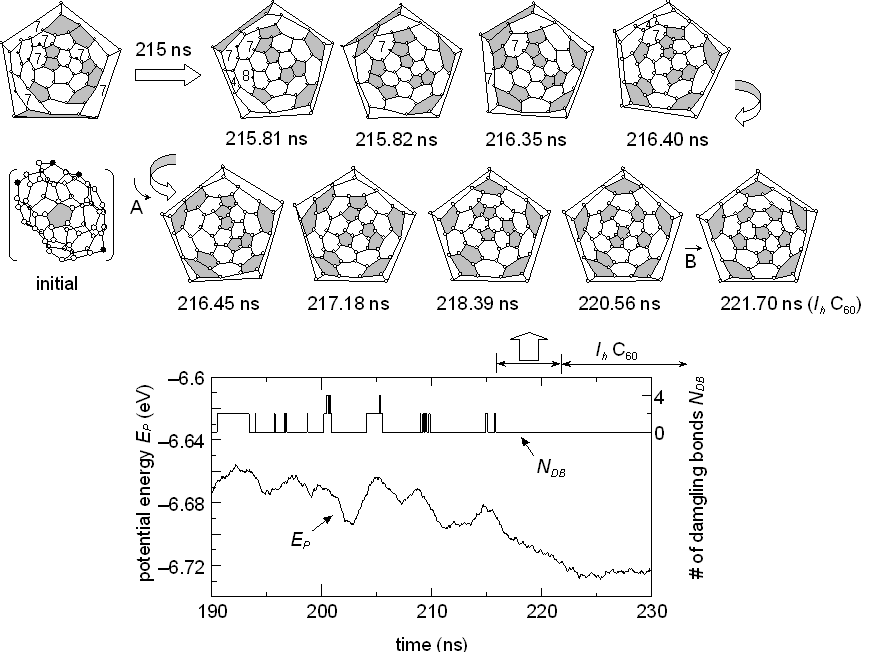
In order to evaluate the effect of the collision-free annealing, the C60 cluster originally obtained in our clustering simulation at 1990 ps (Fig. 2 of [21]) was kept at a high temperature of Tc=2500 K after removing all other atoms and clusters. Transformations of the network structure are shown in Fig. 1, where the Schlegel diagram is adopted: e. g. the 3-dimensional initial structure (marked ‘initial’ in Fig. 1) is expressed with the diagram at top left. The initial structure contained 4 atoms having dangling bonds, neighboring pentagons and 6 heptagons, and was quite different from the perfect fullerene C60 consisted of 20 hexagons and 12 isolated pentagons. The bottom panel of Fig. 1 shows the potential energy per atom EP and the number of dangling bonds NDB during the annealing process. Here, instantaneous dangling bonds that disappeared within 50 ps are omitted. The network structure frequently changed to reduce the strain with infrequent occurrence of generating dangling bonds that induced much higher potential energy. After about 215 ns, no dangling bonds appeared, and migrations of pentagons led the structure to the perfect icosahedral fullerene C60 as shown in the top sequence of Fig. 1. After 221.7 ns, the perfect C60 structure continued to exist for all of 13 ns, until 234.8 ns.
Fig. 1 Annealing process to the perfect C60. Pentagons are marked as gray face. Open and solid symbols represent atoms with three bonds and atoms with a dangling bond, respectively.
Almost all transformations without explicit dangling bonds were explained as Stone-Wales transformations [23] or as generalized S-W transformations [24] as shown in Fig. 2. The configuration of pentagons and hexagons in Fig 2(a) changed through the rotation of the bond between two atoms expressed by empty circles by 90 degrees, which requires only the breakage of two bonds and the creation of two bonds. An example of a similar rearrangement for generalized S-W is also shown in Fig. 2(b). Rather small activation energy for this transformation as estimated by quantum dynamics calculation was recently reported [25].
The C70 perfect structure was also achieved in about 150 ns from the C70 caged cluster in Fig. 2 in our previous report [21] by the same annealing simulation. These are the first demonstrations of the self-assembly of perfect C60 and C70 structures by molecular simulations.
It should be noted that the appearance of dangling bonds was infrequent, i.e. all carbon atoms had three bonds during most of the annealing period. Since the earliest reports of Rohlfing et al. [26] or Kroto et al. [27], the appearance of even numbered positive ions was the unique feature of mass-spectroscopic studies of carbon clusters. From Euler's theorem of geometry, the number of carbon atoms must be even if each carbon atom has three bonds: an additional restriction that all faces are pentagons or hexagons leads to the well-known condition that the number of pentagons is always 12. The molecular dynamics result strongly suggests that the mass-spectroscopic results of even-numbered ions can be regarded as the frozen form of such meta-stable structures as seen in Fig. 1.
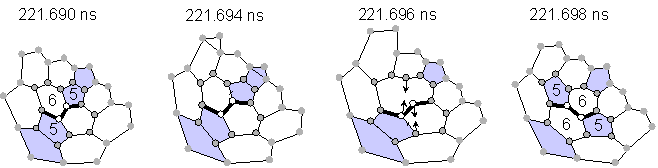
(a) Stone-Wales rearrangement (transformation B in Fig. 1).
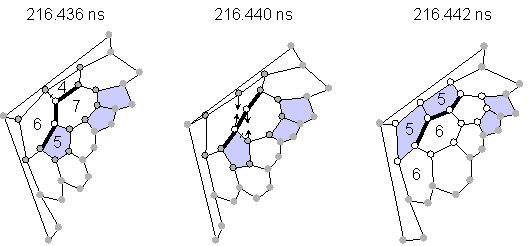
(b) Generalized Stone-Wales rearrangement (transformation A in Fig. 1).
Fig. 2 Network transformations through Stone-Wales rearrangements.
3-2. Discussion of Temperature and Time Scale
The time scale of 200 ns and the temperature of 2500 K for C60 and C70 annealing simulations seem to be unrealistic. The experimental annealing temperature could be estimated to be about 1000~1500 K for the laser irradiation method [2,28] and 1000 K for the arc discharge method [2,29], but in this simulation a high temperature condition of 2500 K was imposed to promote annealing. We therefore estimated the reaction rate of Stone-Wales transformations in C60 to examine the relation between temperature and time. Sixty carbon atoms were initially located at the equilibrium positions of icosahedral C60, and the reaction rate was plotted in Arrhenius style in Fig. 3 for temperature ranges from 2000 K to 3000 K, where bond switching denotes the sum of bond creations and breakages. Both bond switching and pentagon migration rates were plotted in a straight line, and the activation energies of 1.9 eV and 2.5 eV were estimated from the gradient, respectively. If we extrapolate the rate of pentagon migration, the reaction in 200 ns at 2500 K corresponds to ~0.5ms at 1500 K and ~10 s at 1000 K. These orders of time and temperature agree well with the experimental conditions of the laser irradiation method and the arc discharge method, respectively.
This rough extrapolation is very dangerous because it is based on the assumption that the S-W transformation is the only possible single stage reaction regardless of temperature. This assumption can be allowed here because of the large difference between the chemical energy scale and the temperature energy scale. In a sense, this is similar to the concept of multiple time step calculations, and the careful usage of this technique must help to compensate for the time scale problem of general molecular dynamics studies.
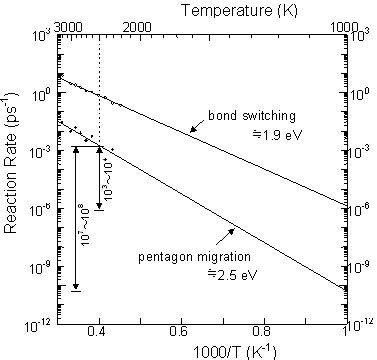
Fig. 3 Arrehenius plot of the S-W transformation and bond switching rates of C60.
3-3. Annealing of Smaller Clusters
The smaller precursors such as C26, C33 and C48 were also picked out from Fig. 2 of our previous simulation [21] and annealed at Tc=3000 K with the same method. Fig. 4 shows typical structures, number of bonds (NB) and potential energy (EP) per atom for C26 and C33. In contrast to C60 and C70, these small clusters did not have any specific structure that was most stable and frequently changed structures as shown in Fig. 4. For C26 [Fig. 4 (a)], a flat structure was preferred to a tangled polycyclic structure. The flat structures were energetically more stable as shown in the bottom diagram, because the tangled structures would induce more stress while the number of bonds was almost the same for both structures. On the other hand, the C33 [Fig. 4 (b)] changed back and forth between flat and random caged structures. The probability to choose these two structures seemed to be the same, though a random cage was energetically more stable due to the reduction of dangling bonds. The choice of the energetically unfavorable flat structure was possible because of the entropy effect at this temperature: there were a large variety of flat structures compared to the unique condensed random caged structure. These results show a very good comparison with the recent result of tight-binding calculation [30], which gives much more reliable energy for a limited number of structures.
When the clustering simulation was performed under lower temperature conditions, the initial flat structure could not overcome the energy barrier to transform to the random caged structure [21]. On the other hand, under a high temperature condition, the chaotic 3-dimensional structure was more likely [21].
Fig. 4 Dynamic structures of smaller precursor clusters at Tc=3000 K.
4. Fullerene Formation Model
Considering current results and the temperature dependence of the cluster structure [21], we propose a new fullerene formation model as seen in Fig. 5.
The graphite source is initially decomposed into atoms or dimers by a laser irradiation or an arc discharge method. Upon cooling, these carbon clusters grow larger from simple structures like chains or rings for Cn (n<20), and flat structures for around Cn (20<n<30). Then, the cluster meets the turning point at around C30; if the temperature is too low, it grows larger keeping the flat structure, while if the temperature is too high, a tangled polycyclic structure is favored. Only when an adequate temperature condition or cooling rate is applied can they rearrange to a hollow random caged structure. However, at that size, the number of carbon atoms is not enough to form a closed cage, and dangling bonds remain. Then, this grows larger while rearranging the network structure during the collision-free interval, which is relatively long due to its small collisional cross section, and finally reaches the perfect fullerene C60 satisfying the IPR. If it fails to become C60 by inappropriate addition, C70 will be the second candidate. Assuming that the perfect fullerene satisfying the IPR is not reactive to further collisions, C60 can be the most probable fullerene at which the growth stops.
The structures from C20 to C40 in our model do not look so sophisticated as the precursors in the “pentagon road” model [2,6]. The whole process is similar to the “fullerene road” model [10], however, we propose the meta-stable random caged structure in which all atoms can have three bonds. This will overcome the problem of the “fullerene road”: the unlikely assumption of C2 addition in the correct position between adjacent pentagons. Moreover, our model contradicts neither the ion-chromatography experiments [11,12] where the tri-cyclic structured C60 was assumed as the precursor, nor the experimental result obtained using naphthalene [20].
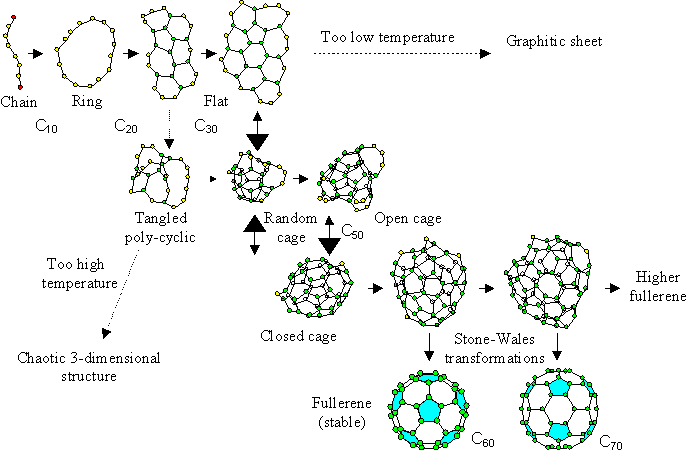
Fig. 5 Proposed fullerene formation model.
5. Conclusions
The annealing process of a C60 cluster was simulated from an initial structure obtained in a clustering simulation from isolated carbon atoms. The prefect fullerene C60 and C70 structures were achieved through Stone-Wales transformations under reasonable time and temperature conditions. The preferred dynamic structures of small precursor clusters were also studied. Considering these results, a new fullerene formation model was proposed and compared with previously reported models.
Acknowledgements
This work was supported by a Grant-in-Aid for JSPS Fellows (No.08004746) from the Ministry of Education, Science, Sports and Culture, Japan.
References